
【題目】甲,乙兩人同時各接受了600個零件的加工任務,甲比乙每分鐘加工的數量多,兩人同時開始加工,加工過程中其中一人因故障停止加工幾分鐘后又繼續按原速加工,直到他們完成任務,如圖表示甲比乙多加工的零件數量![]() (個)與加工時間
(個)與加工時間![]() (分)之間的函數關系,觀察圖象解決下列問題:
(分)之間的函數關系,觀察圖象解決下列問題:
(1)點B的坐標是________,B點表示的實際意義是___________ _____;
(2)求線段BC對應的函數關系式和D點坐標;
(3)乙在加工的過程中,多少分鐘時比甲少加工100個零件?
(4)為了使乙能與甲同時完成任務,現讓丙幫乙加工,直到完成.丙每分鐘能加工3個零件,并把丙加工的零件數記在乙的名下,問丙應在第多少分鐘時開始幫助乙?并在圖中用虛線畫出丙幫助后y與x之間的函數關系的圖象.
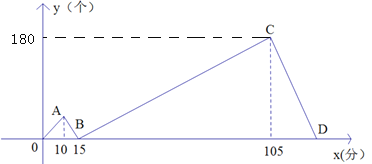
【答案】(1)B(15,0),甲乙兩人工作15分鐘時,加工零件的數量相同
(2)y=2x-30,D(150,0)(3)65分鐘或125分鐘(4)第45分鐘
【解析】試題分析:(1)觀察圖象即可得出點B的坐標,然后根據縱坐標的意義可知此時兩人加工的零件數量相同;
(2)利用待定系數法即可得BC對應的函數關系式,根據圖象可知105分鐘時甲完成任務,甲實際用了100分鐘完成任務,從而得到甲的速度,繼而知道乙的速度,從而得出點D坐標;
(3)求出CD段的解析式,分別所y=100代入BC、CD段解析式即可得;
(4)設丙應該在x分鐘時加入,根據等量關系:乙x分鐘加工的數量+乙、丙(105-x)分鐘加工的數量=600,解方程即可得,然后補全圖象即可.
試題解析:(1)由圖象可知B(15,0),根據縱軸表示甲比乙多加工的零件數量可知此時甲、乙加工的零件數量相同,
故答案為:(15,0),甲乙兩人工作15分鐘時,加工零件的數量相同;
(2)設直線BC的解析式為:y=kx+b,由題意則有
![]() ,解得:
,解得: ![]() ,所以BC段的函數關系式為:y=2x-30,
,所以BC段的函數關系式為:y=2x-30,
由圖象可知105分鐘時甲完成了任務,甲中間休息了5分鐘,105-5=100,
600÷100=6,6-2=4,600÷4=150,所以D(150,0);
(3)把y=100代入y=2x-30,得:100=2x-30,解得:x=65,
設直線CD的解析式為:y=ax+e,由題意則有
![]() ,解得:
,解得: ![]() ,所以BC的函數關系式為:y=-4x+600,
,所以BC的函數關系式為:y=-4x+600,
當y=100時,有100=-4x+600,解得:x=125,
所以乙在加工的過程中,65或125分鐘時比甲少加工100個零件;
(4)設x分鐘時丙加入,則有:4x+(4+3)(105-x)=600,解得:x=45,
即:丙在45分鐘時開始幫助乙,
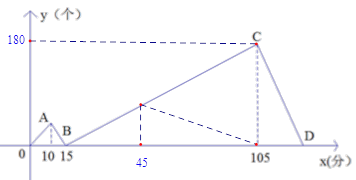
圖象如圖所示:


 一課一練課時達標系列答案
一課一練課時達標系列答案科目:初中數學 來源: 題型:
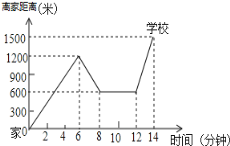
【題目】“珍重生命,注意安全!”同學們在上下學途中一定要注意騎車安全.小明騎單車上學,當他騎了一段時,想起要買某本書,于是又折回到剛經過的新華書店,買到書后繼續去學校,以下是他本次所用的時間與路程的關系示意圖.根據圖中提供的信息回答下列問題:
(1)小明家到學校的路程是多少米;
(2)小明在書店停留了多少分鐘;
(3)本次上學途中,小明一共行駛了多少米?一共用了多少分鐘?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上兩點![]() ,
,![]() (點
(點![]() 在點
在點![]() 的右側),若數軸上存在一點
的右側),若數軸上存在一點![]() ,使得
,使得![]() ,則稱點
,則稱點![]() 為點
為點![]() ,
,![]() 的“
的“![]() 倍分點”,若使得
倍分點”,若使得![]() ,則稱點
,則稱點![]() 為點
為點![]() ,
,![]() 的“
的“![]() 倍分點”,
倍分點”,![]() ,若使得
,若使得![]() ,則稱點
,則稱點![]() 為點
為點![]() ,
,![]() 的“
的“![]() 倍分點(
倍分點(![]() 為正整數).請根據上述規定回答下列問題:
為正整數).請根據上述規定回答下列問題:
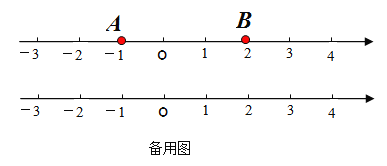
(1)如圖,若點![]() 表示數
表示數![]() ,點
,點![]() 表示數
表示數![]() .
.
①當點![]() 表示數
表示數![]() 時,則
時,則![]() _______;
_______;
②當點![]() 為點
為點![]() ,
,![]() 的“
的“![]() 倍分點”時,求點
倍分點”時,求點![]() 表示的數;
表示的數;
(2)若點![]() 表示數
表示數![]() ,
,![]() ,當點
,當點![]() 為
為![]() 的“
的“![]() 倍分點”時,請直接寫出點
倍分點”時,請直接寫出點![]() 表示的數.(用含
表示的數.(用含![]() 的代數式表示)
的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠接受了20天內生產1200臺GH型電子產品的總任務.已知每臺GH型產品由4個G型裝置和3個H型裝置配套組成.工廠現有80名工人,每個工人每天能加工6個G型裝置或3個H型裝置.工廠將所有工人分成兩組同時開始加工,每組分別加工一種裝置,并要求每天加工的G、H型裝置數量正好全部配套組成GH型產品.
(1)按照這樣的生產方式,工廠每天能配套組成多少套GH型電子產品?請列出二元一次方程組解答此問題.
(2)為了在規定期限內完成總任務,工廠決定補充一些新工人,這些新工人只能獨立進行G型裝置的加工,且每人每天只能加工4個G型裝置.1.設原來每天安排x名工人生產G型裝置,后來補充m名新工人,求x的值(用含m的代數式表示)2.請問至少需要補充多少名新工人才能在規定期內完成總任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為1,AC,BD是對角線,將△DCB繞著點D順時針旋轉45°得到△DGH,HG交AB于點E,連接DE交AC于點F,連接FG.則下列結論:
①四邊形AEGF是菱形;②△HED的面積是1﹣![]() ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG=![]() .其中正確的結論是( )
.其中正確的結論是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】原題呈現:若 a ![]() b
b![]() 4a 2b 5 0 ,求 a、b 的值.方法介紹:
4a 2b 5 0 ,求 a、b 的值.方法介紹:
①看到 a ![]() 4a 可想到如果添上常數 4 恰好就是 a
4a 可想到如果添上常數 4 恰好就是 a ![]() 4a 4 (a 2)
4a 4 (a 2)![]() ,這個過程叫做“配方”,同理 b
,這個過程叫做“配方”,同理 b ![]() 2b 1 (b 1)
2b 1 (b 1) ![]() ,恰好把常數5分配完;
,恰好把常數5分配完;
②從而原式可以化為(a 2)![]() (b 1)
(b 1)![]() 0 由平方的非負性可得 a 2 0 且 b 1 0.經驗運用:
0 由平方的非負性可得 a 2 0 且 b 1 0.經驗運用:
(1)若 4a ![]() b
b![]() 20a 6b 34 0 求 a b 的值;
20a 6b 34 0 求 a b 的值;
(2)若 a![]() 5b
5b![]() c
c ![]() 2ab 4b 6c 10 0 求 a b c 的值.
2ab 4b 6c 10 0 求 a b c 的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com