提高過江大橋的車輛通行能力可改善整個城市的交通狀況.在一般情況下,大橋上的車流速度v(單位:千米/時)是車流密度x(單位:輛/千米)的函數,當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/時.研究表明:當20≤x≤200時,車流速度v是車流密度x的一次函數.
(l)當0≤x≤200時,求車流速度v關于x的解析式;
(2)當車流密度x為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/時,車流量=車流密度×車流速度)可以達到最大,并求出最大值(精確到1輛/時).
【答案】
分析:(1)根據題意,函數v(x)表達式為分段函數的形式,關鍵在于求函數v(x)在20≤x≤200時的表達式,根據一次函數表達式的形式,用待定系數法可求得;
(2)先在0≤x≤20上,車流量函數為增函數,得最大值為v(20)=1200,然后在20≤x≤200上,車流量函數為二次函數,然后根據二次函數的最大值問題解答.
解答:解:(1)由題意:當0≤x≤20時,v=60,
當20<x≤200時,設v=kx+b,
根據題意得,
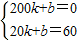
,
解得
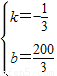
,
所以,函數解析式為v=-

x+
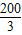
,
故車流速度v關于x的解析式為v=
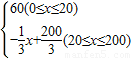
;
(2)依題并由(1)可得車流量v(x)=60x(0≤x<20),
v(x)=x(-

x+
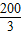
)=-

(x-100)
2+
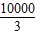
,(20≤x≤200),
當0≤x<20時,v(x)為增函數,故當x=20時,其最大值為60×20=1200,
當20≤x≤200時,當x=100時,v(x)最大,最大值為=
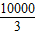
≈3333,
綜上所述,當x=100時,最大值約為3333.
答:(1)函數v關于x的解析式為v=
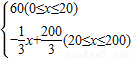
;
(2)x=100時,最大值約為3333.
點評:本題主要考查一次函數的應用、最值等基礎知識,同時考查運用數學知識解決實際問題的能力,屬于中等題.

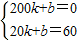 ,
,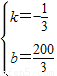 ,
, x+
x+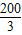 ,
,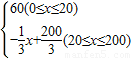 ;
; x+
x+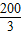 )=-
)=- (x-100)2+
(x-100)2+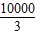 ,(20≤x≤200),
,(20≤x≤200),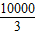 ≈3333,
≈3333,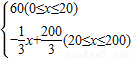 ;
;

