
如圖,在平面直角坐標系中,拋物線 經過點A(3,0)、B(0,-3),點P是直線AB上的動點,過點P作x軸的垂線交拋物線于點M,設點P的橫坐標為t.
經過點A(3,0)、B(0,-3),點P是直線AB上的動點,過點P作x軸的垂線交拋物線于點M,設點P的橫坐標為t.

(1)分別求出直線AB和這條拋物線的解析式.(4分)
(2)若點P在第四象限,連接AM、BM,當線段PM最長時,求△ABM的面積.(4分)
(3)是否存在這樣的點P,使得以點P、M、B、O為頂點的四邊形為平行四邊形?若存在,請直接寫出點P的橫坐標;若不存在,請說明理由(4分)
(1) ;(2)
;(2) ; (3)存在,P點的橫坐標是
; (3)存在,P點的橫坐標是 或
或 .
.
【解析】
試題分析:(1)分別利用待定系數法求兩函數的解析式:把A(3,0)B(0,﹣3)分別代入 與
與 ,得到關于m、n的兩個方程組,解方程組即可;
,得到關于m、n的兩個方程組,解方程組即可;
(2)設點P的坐標是( ,
, ),則M(
),則M( ,
, ),用P點的縱坐標減去M的縱坐標得到PM的長,即PM=(
),用P點的縱坐標減去M的縱坐標得到PM的長,即PM=( )﹣(
)﹣( )=
)= ,然后根據二次函數的最值得到
,然后根據二次函數的最值得到
當 時,PM最長為
時,PM最長為 ,再利用三角形的面積公式利用S△ABM=S△BPM+S△APM計算即可;
,再利用三角形的面積公式利用S△ABM=S△BPM+S△APM計算即可;
(3)由PM∥OB,根據平行四邊形的判定得到當PM=OB時,點P、M、B、O為頂點的四邊形為平行四邊形,然后討論:當P在第四象限:PM=OB=3,PM最長時只有 ,所以不可能;當P在第一象限:PM=OB=3,(
,所以不可能;當P在第一象限:PM=OB=3,( )﹣(
)﹣( )=3;當P在第三象限:PM=OB=3,
)=3;當P在第三象限:PM=OB=3, ,分別解一元二次方程即可得到滿足條件的t的值.
,分別解一元二次方程即可得到滿足條件的t的值.
試題解析:(1)把A(3,0)B(0,﹣3)代入 ,得:
,得: ,解得
,解得 ,
,
所以拋物線的解析式是 .
.
設直線AB的解析式是 ,
,
把A(3,0)B(0,﹣3)代入 ,得:
,得: ,解得:
,解得: ,
,
所以直線AB的解析式是 ;
;
(2)設點P的坐標是( ,
, ),則M(
),則M( ,
, ),因為p在第四象限,
),因為p在第四象限,
所以PM=( )﹣(
)﹣( )=
)= ,
,
當 時,二次函數的最大值,即PM最長值為
時,二次函數的最大值,即PM最長值為 ,
,
則S△ABM=S△BPM+S△APM= ;
;
(3)存在,理由如下:∵PM∥OB,
∴當PM=OB時,點P、M、B、O為頂點的四邊形為平行四邊形,
①當P在第四象限:PM=OB=3,PM最長時只有 ,所以不可能有PM=3.
,所以不可能有PM=3.
②當P在第一象限:PM=OB=3,( )﹣(
)﹣( )=3,解得
)=3,解得 ,
, (舍去),所以P點的橫坐標是
(舍去),所以P點的橫坐標是 ;
;
③當P在第三象限:PM=OB=3, ,解得
,解得 (舍去),
(舍去), ,所以P點的橫坐標是
,所以P點的橫坐標是 .所以P點的橫坐標是
.所以P點的橫坐標是 或
或 .
.

考點:1.二次函數綜合題;2.平行四邊形的判定.


科目:初中數學 來源:2014-2015學年湖北省七年級上學期期中考試數學試卷(解析版) 題型:選擇題
如果收入80元記作+80元,那么支出20元記作( )
A.+20元 B.﹣20元 C.+100元 D.﹣100元
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖南省婁底市八年級上學期期中聯考數學試卷(解析版) 題型:選擇題
如圖,△ABC≌△EFD且AB=EF,CE=3.5,CD=3,則AC=( )
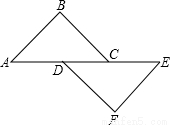
A. 3 B.3.5 C.6.5 D.5
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖南省婁底市名校九年級上學期第二次聯考數學試卷(解析版) 題型:選擇題
下列結論中正確的是( )
A.兩個正方形一定相似 B.兩個菱形一定相似
C.兩個等腰梯形一定相似 D.兩個直角梯形一定相似
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖南省岳陽市九年級上學期第二次月考數學試卷(解析版) 題型:填空題
如圖,△ABC與△A’B’C’是位似圖形,且位似比是1:2,若AB=2cm,則A’B’= cm。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com