
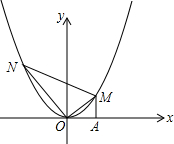
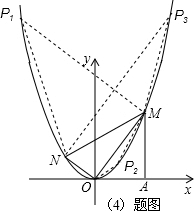
 ,設(shè)M、N的橫坐標分別為m、n(m>0,n<0);請解答下列問題:
,設(shè)M、N的橫坐標分別為m、n(m>0,n<0);請解答下列問題: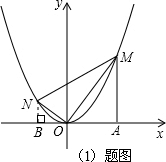 解:(1)當m=1時,點M的坐標為(1,1),點N的坐標為(n,n2),
解:(1)當m=1時,點M的坐標為(1,1),點N的坐標為(n,n2), =
=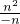 ,
, =
=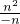 ,
, ;
;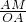 =
=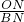 ,
,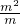 =
=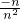 ,
,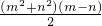 -
-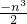 -
-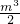 ,
,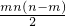 ,
,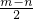 ,
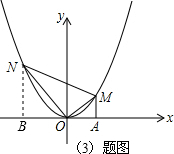
,
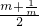 ,
,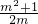 ;
;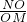 ,
,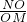 =
= ,
,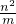 =
= ,
, ,
, m•m2=
m•m2= m3=
m3= ;
; =-
=- ,
, ,
, ),
), x,OM的解析式為y=2x,
x,OM的解析式為y=2x,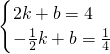 ,
,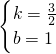 ,
,
 x+1,
x+1, x+e,
x+e, ×2+e=4,
×2+e=4, x+5,
x+5,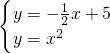 ,
,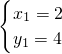 (為點M),
(為點M),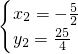 ,
, ,
, );
); x,
x,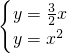 ,
,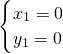 (為點O),
(為點O),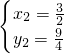 ,
, ,
, );
); )+f=
)+f= ,
, ,
, ,
,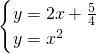 ,
,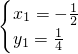 (為點N),
(為點N),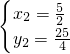 ,
, ,
, ),
), ,
, )或(
)或( ,
, )或(
)或( ,
, )時,M、N、O、P四點構(gòu)成梯形.
)時,M、N、O、P四點構(gòu)成梯形.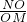 ,再根據(jù)△OMA和△NOB相似,利用相似三角形對應(yīng)邊成比例列式求出m、n的關(guān)系,然后把m•n=-1代入消掉n,再根據(jù)三角形的面積公式列式整理即可得解;
,再根據(jù)△OMA和△NOB相似,利用相似三角形對應(yīng)邊成比例列式求出m、n的關(guān)系,然后把m•n=-1代入消掉n,再根據(jù)三角形的面積公式列式整理即可得解;

 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:
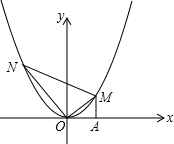 ,設(shè)M、N的橫坐標分別為m、n(m>0,n<0);請解答下列問題:
,設(shè)M、N的橫坐標分別為m、n(m>0,n<0);請解答下列問題:| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:

| 2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

 (如圖1),求a的值;
(如圖1),求a的值;查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
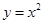 交于M、N兩點,設(shè)M、N的橫坐標分別為m、n(m﹥0,n﹤0);請解答下列問題:
交于M、N兩點,設(shè)M、N的橫坐標分別為m、n(m﹥0,n﹤0);請解答下列問題:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2012年江西省贛州市定南縣三中片區(qū)九年級數(shù)學(xué)全能競賽試卷(解析版) 題型:解答題

 (如圖1),求a的值;
(如圖1),求a的值;查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com