
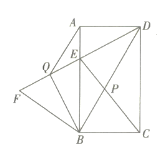
【題目】如圖,在矩形![]() 中,連接
中,連接![]() 點
點![]() 為
為![]() 上一點,使得
上一點,使得![]() 連接
連接![]() 交
交![]() 于點
于點![]() ,作
,作![]() 交
交![]() 的延長線于點
的延長線于點![]() .
.
(1)求證:![]() .
.
(2)若![]() 求
求![]() 的長.
的長.
(3)在(2)的條件下,將![]() 沿著
沿著![]() 對折得到
對折得到![]() 點
點![]() 的對應點為點
的對應點為點![]() ,連接
,連接![]() 試求
試求![]() 的周長.
的周長.
【答案】(1)詳見解析;(2)![]() ;(3)
;(3)![]() 的周長
的周長![]()
【解析】
(1)由矩形的性質得∠BCD=∠FBD,結合∠BCD=∠FBD,可得![]() ,進而即可得到結論;
,進而即可得到結論;
(2)先證![]() ,再證BE=DE=EF,結合
,再證BE=DE=EF,結合![]() ,求出BD的長,從而的BC,EC的長,由
,求出BD的長,從而的BC,EC的長,由![]() ,得
,得![]() ,即可求解;
,即可求解;
(3)由折疊的性質得QE=1,從而得AE=QE,再證![]() ,進而即可求解.
,進而即可求解.
(1)∵在矩形![]() 中,
中,
∴∠BCD=90°,
∵![]() ,
,
∴∠BCD=∠FBD,
又∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]()
![]() .
.
![]() ,
,
![]() ,
,
由(1)可知:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
解得:![]() ;
;
(3)![]() 沿
沿![]() 對折得到
對折得到![]() ,
,![]() ,
,
![]() 點
點![]() 在
在![]() 上,且
上,且![]() ,
,
∴DQ=DC=3,
∵DE=BE=2,
![]() ,
,
![]() ,
,
![]() .
.
∵BE=DE,
∴∠EBD=∠EDB,
又![]() ,
,
∴![]() =∠EBD=∠EDB,
=∠EBD=∠EDB,
![]() ,
,
![]() 的周長:
的周長:![]() 的周長
的周長![]() ,
,
![]() 的周長
的周長![]() ,
,
![]() 的周長
的周長![]() .
.


科目:初中數學 來源: 題型:
【題目】(1)問題發現如圖1,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,連接
,連接![]() 交于點
交于點![]() .填空:①
.填空:①![]() 的值為______;②
的值為______;②![]() 的度數為______.
的度數為______.
(2)類比探究如圖2,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,連接
,連接![]() 交
交![]() 的延長線于點
的延長線于點![]() .請判斷
.請判斷![]() 的值及
的值及![]() 的度數,并說明理由;
的度數,并說明理由;
(3)拓展延伸在(2)的條件下,將![]() 繞點
繞點![]() 在平面內旋轉,
在平面內旋轉,![]() 所在直線交于點
所在直線交于點![]() ,若
,若![]() ,
,![]() ,請直接寫出當點
,請直接寫出當點![]() 與點
與點![]() 在同一條直線上時
在同一條直線上時![]() 的長.
的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D、F分別是BC、AC邊的中點,連接DA、DF,且AD=2DF,過點B作AD的平行線交FD的延長線于點E.
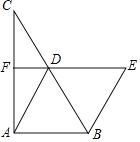
(1)求證:四邊形ABED為菱形;
(2)若BD=6,∠E=60°,求四邊形ABEF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,李林和王聰兩人在玩轉盤游戲時,分別把轉盤![]() ,
,![]() 分成3等份和4等份,并標上數字(如圖所示).游戲規則:同時轉動兩個轉盤,當兩轉盤停止后,若指針所指兩個數字之和小于4,則李林獲勝;若數字之和大于4,則王聰獲勝,如果指針落在分割線上,則需要重新轉動轉盤.
分成3等份和4等份,并標上數字(如圖所示).游戲規則:同時轉動兩個轉盤,當兩轉盤停止后,若指針所指兩個數字之和小于4,則李林獲勝;若數字之和大于4,則王聰獲勝,如果指針落在分割線上,則需要重新轉動轉盤.
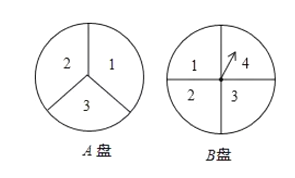
(1)用列表法或畫樹狀圖法中的一種方法,求所有可能出現的結果.
(2)該游戲規則對雙方公平嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
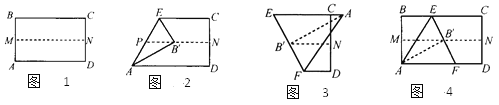
【題目】取一張矩形紙片進行折疊,具體操作過程如下:第一步:先把矩形ABCD對折,折痕為MN,如圖1;第二步:再把B點疊在折痕線MN上,折痕為AE,點B在MN上的對應點為B',得Rt△AB'E,如圖2;第三步:沿EB'線折疊得折痕EF,使A點落在EC的延長線上,如圖3.
利用展開圖4探究:
(1)△AEF是什么三角形?證明你的結論;
(2)對于任一矩形,按照上述方法是否都能折出這種三角形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校調查了若干名家長對“初中生帶手機上學”現象的看法,統計整理并制作了如下的條形與扇形統計圖,根據圖中提供的信息,完成以下問題:
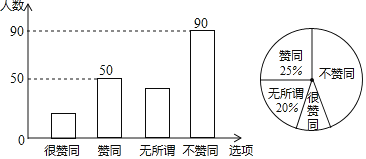
(1)本次共調查了 名家長;扇形統計圖中“很贊同”所對應的圓心角是 度.已知該校共有1600名家長,則“不贊同”的家長約有 名;請補全條形統計圖;
(2)從“不贊同”的五位家長中(兩女三男),隨機選取兩位家長對全校家長進行“學生使用手機危害性”的專題講座,請用樹狀圖或列表法求出選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了綠化環境,某中學八年級(3班)同學都積極參加了植樹活動,下面是今年3月份該班同學植樹情況的扇形統計圖和不完整的條形統計圖:
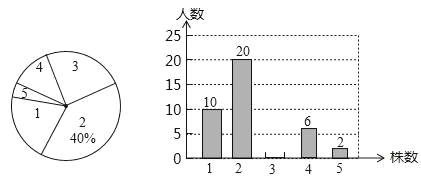
請根據以上統計圖中的信息解答下列問題.
(1)植樹3株的人數為 ;
(2)扇形統計圖中植樹為1株的扇形圓心角的度數為 ;
(3)該班同學植樹株數的中位數是
(4)小明以下方法計算出該班同學平均植樹的株數是:(1+2+3+4+5)÷5=3(株),根據你所學的統計知識
判斷小明的計算是否正確,若不正確,請寫出正確的算式,并計算出結果
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,圓柱形玻璃杯高為![]() ,底面周長為
,底面周長為![]() ,在杯內壁離杯底
,在杯內壁離杯底![]() 的點
的點![]() 處有一滴蜂蜜,此時一只螞蟻正好在杯外壁上,它在離杯上沿
處有一滴蜂蜜,此時一只螞蟻正好在杯外壁上,它在離杯上沿![]() 且與蜂蜜相對的
且與蜂蜜相對的![]() 處,則螞蟻從外壁
處,則螞蟻從外壁![]() 處走到內壁
處走到內壁![]() 處,至少爬多少厘米才能吃到蜂蜜( )
處,至少爬多少厘米才能吃到蜂蜜( )
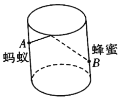
A.24B.25C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com