
【題目】綜合與實(shí)踐
折紙是同學(xué)們喜歡的手工活動(dòng)之一,通過折紙我們既可以得到許多美麗的圖形,同時(shí)折紙的過程還蘊(yùn)含著豐富的數(shù)學(xué)知識(shí).
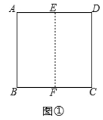
折一折:把邊長(zhǎng)為4的正方形紙片![]() 對(duì)折,使邊
對(duì)折,使邊![]() 與
與![]() 重合,展開后得到折痕
重合,展開后得到折痕![]() .如圖①:
.如圖①:![]() 為
為![]() 上一點(diǎn),將正方形紙片
上一點(diǎn),將正方形紙片![]() 沿直線
沿直線![]() 折疊,使點(diǎn)
折疊,使點(diǎn)![]() 落在
落在![]() 的點(diǎn)
的點(diǎn)![]() 處,展開后連接
處,展開后連接![]() ,如圖②
,如圖②
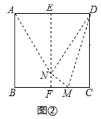
(一)做一做:
(1)圖②中,求![]() 的度數(shù)和線段
的度數(shù)和線段![]() 的長(zhǎng)度.
的長(zhǎng)度.
(2)圖②中,試判斷![]() 的形狀,并給出證明.
的形狀,并給出證明.
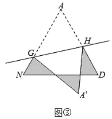
剪一剪、折一折:將圖②中的![]() 剪下來,將其沿直線
剪下來,將其沿直線![]() 折疊,使點(diǎn)
折疊,使點(diǎn)![]() 落在點(diǎn)
落在點(diǎn)![]() 處,分別得到圖③、圖④.
處,分別得到圖③、圖④.
(二)填一填:
(3)圖③中陰影部分的周長(zhǎng)為________.
(4)圖③中,若![]() ,則
,則![]() __________
__________![]() .
.
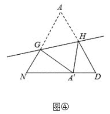
(5)如圖④點(diǎn)![]() 落在邊
落在邊![]() 上,若
上,若![]() ,則
,則![]() ______(用含
______(用含![]() 的代數(shù)式表示).
的代數(shù)式表示).
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 是等邊三角形,理由詳見解析;(3)12;(4)
是等邊三角形,理由詳見解析;(3)12;(4)![]() ;(5)
;(5)![]()
【解析】
(1)由折疊得四邊形CDEF是矩形,ED=![]() AD=2,DN=CD=4,求出∠CDN=∠END=30°,
AD=2,DN=CD=4,求出∠CDN=∠END=30°,
由折疊得∠CDM=∠NDM得到∠CDM=15°,根據(jù)∠CMD=90°-∠CDM求出度數(shù),根據(jù)EN=![]() ,EF=CD=4,求出NF=
,EF=CD=4,求出NF=![]() ;
;
(2)![]() 是等邊三角形;由折疊得AE=DE,∠AEN=∠DEN=90°,證得
是等邊三角形;由折疊得AE=DE,∠AEN=∠DEN=90°,證得![]() ,得到
,得到![]() ,再求出∠AND=90°-∠CDN=60°,即可得到△AND是等邊三角形;
,再求出∠AND=90°-∠CDN=60°,即可得到△AND是等邊三角形;
(3)根據(jù)等邊三角形的性質(zhì)得到AN=ND=AD=4,陰影部分的周長(zhǎng)=NG+![]() +
+![]() +DH+ND=AN+AD+ND即可求出答案;
+DH+ND=AN+AD+ND即可求出答案;
(4)由![]() ,求出
,求出![]() ,利用四邊形的內(nèi)角和360°求出
,利用四邊形的內(nèi)角和360°求出![]() 再根據(jù)鄰補(bǔ)角求出答案;
再根據(jù)鄰補(bǔ)角求出答案;
(5)根據(jù)![]() 設(shè)
設(shè)![]() ,
,![]() (b>0),得到AN=ND=AD=b(m+n),證明△
(b>0),得到AN=ND=AD=b(m+n),證明△![]() ∽△
∽△![]() ,得到
,得到![]() =
=![]() ,即可求出答案.
,即可求出答案.
(1)由折疊得四邊形CDEF是矩形,ED=![]() AD=2,DN=CD=4,
AD=2,DN=CD=4,
∵∠DEF=90°,ED=![]() DN,
DN,
∴∠END=30°,
∴∠CDN=∠END=30°,
由折疊得∠CDM=∠NDM,
∴∠CDM=15°,
∴∠CMD=90°-∠CDM=75°,
∵EN=![]() ,EF=CD=4,
,EF=CD=4,
∴NF=![]() ;
;
(2)![]() 是等邊三角形;
是等邊三角形;
證明:由折疊得AE=DE,∠AEN=∠DEN=90°,
又∵EN=EN,
∴![]() ,
,
∴![]() ,
,
∵∠AND=90°-∠CDN=60°,
∴△AND是等邊三角形;
(3)∵△AND是等邊三角形,
∴AN=ND=AD=4,
∴陰影部分的周長(zhǎng)=NG+![]() +
+![]() +DH+ND=AN+AD+ND=12,
+DH+ND=AN+AD+ND=12,
故答案為:12;
(4)∵![]() ,
,
∴![]() ,
,
∵∠A=![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案為:![]() ;
;
(5)∵![]() ,
,
∴設(shè)![]() ,
,![]() (b>0),
(b>0),
∵△AND是等邊三角形,
∴AN=ND=AD=b(m+n),
∵![]() ,
,
∴![]() ,
,
∵∠N=∠D=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
=![]() .
.
∴![]()
![]() ,
,
故答案為:![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直角三角形的直角頂點(diǎn)在坐標(biāo)原點(diǎn),∠OAB=30°,若點(diǎn) A 在反比例函數(shù)![]() (x>0)的圖象上,則經(jīng)過點(diǎn) B 的反比例函數(shù)解式為_________.
(x>0)的圖象上,則經(jīng)過點(diǎn) B 的反比例函數(shù)解式為_________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知正方形ABCD與正方形CEFG,M是AF的中點(diǎn),連接DM,EM.
(1)如圖1,點(diǎn)E在CD上,點(diǎn)G在BC的延長(zhǎng)線上,請(qǐng)判斷DM,EM的數(shù)量關(guān)系與位置關(guān)系,并直接寫出結(jié)論;
(2)如圖2,點(diǎn)E在DC的延長(zhǎng)線上,點(diǎn)G在BC上,(1)中結(jié)論是否仍然成立?請(qǐng)證明你的結(jié)論;
(3)將圖1中的正方形CEFG繞點(diǎn)C旋轉(zhuǎn),使D,E,F(xiàn)三點(diǎn)在一條直線上,若AB=13,CE=5,請(qǐng)畫出圖形,并直接寫出MF的長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】模具廠計(jì)劃生產(chǎn)面積為4,周長(zhǎng)為m的矩形模具.對(duì)于m的取值范圍,小亮已經(jīng)能用“代數(shù)”的方法解決,現(xiàn)在他又嘗試從“圖形”的角度進(jìn)行探究,過程如下:
(1)建立函數(shù)模型
設(shè)矩形相鄰兩邊的長(zhǎng)分別為x,y,由矩形的面積為4,得![]() ,即
,即![]() ;由周長(zhǎng)為m,得
;由周長(zhǎng)為m,得![]() ,即
,即![]() .滿足要求的
.滿足要求的![]() 應(yīng)是兩個(gè)函數(shù)圖象在第 象限內(nèi)交點(diǎn)的坐標(biāo).
應(yīng)是兩個(gè)函數(shù)圖象在第 象限內(nèi)交點(diǎn)的坐標(biāo).
(2)畫出函數(shù)圖象
函數(shù)![]() 的圖象如圖所示,而函數(shù)
的圖象如圖所示,而函數(shù)![]() 的圖象可由直線
的圖象可由直線![]() 平移得到.請(qǐng)?jiān)谕恢苯亲鴺?biāo)系中直接畫出直線
平移得到.請(qǐng)?jiān)谕恢苯亲鴺?biāo)系中直接畫出直線![]() .
.
(3)平移直線![]() ,觀察函數(shù)圖象
,觀察函數(shù)圖象
①當(dāng)直線平移到與函數(shù)![]() 的圖象有唯一交點(diǎn)
的圖象有唯一交點(diǎn)![]() 時(shí),周長(zhǎng)m的值為 ;
時(shí),周長(zhǎng)m的值為 ;
②在直線平移過程中,交點(diǎn)個(gè)數(shù)還有哪些情況?請(qǐng)寫出交點(diǎn)個(gè)數(shù)及對(duì)應(yīng)的周長(zhǎng)m的取值范圍.
(4)得出結(jié)論
若能生產(chǎn)出面積為4的矩形模具,則周長(zhǎng)m的取值范圍為 .

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】今年某市為創(chuàng)評(píng)“全國(guó)文明城市”稱號(hào),周末團(tuán)市委組織志愿者進(jìn)行宣傳活動(dòng).班主任梁老師決定從4名女班干部(小悅、小惠、小艷和小倩)中通過抽簽的方式確定2名女生去參加.
抽簽規(guī)則:將4名女班干部姓名分別寫在4張完全相同的卡片正面,把四張卡片背面朝上,洗勻后放在桌面上,梁老師先從中隨機(jī)抽取一張卡片,記下姓名,再從剩余的3張卡片中隨機(jī)抽取第二張,記下姓名.
(1)該班男生“小剛被抽中”是 事件,“小悅被抽中”是 事件(填“不可能”或“必然”或“隨機(jī)”);第一次抽取卡片“小悅被抽中”的概率為 ;
(2)試用畫樹狀圖或列表的方法表示這次抽簽所有可能的結(jié)果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)![]() 圖象的一部分如圖所示,頂點(diǎn)坐標(biāo)為
圖象的一部分如圖所示,頂點(diǎn)坐標(biāo)為![]() ,與
,與![]() 軸的一個(gè)交點(diǎn)的坐標(biāo)為(-3,0),給出以下結(jié)論:①
軸的一個(gè)交點(diǎn)的坐標(biāo)為(-3,0),給出以下結(jié)論:①![]() ;②
;②![]() ;③若
;③若![]() 、
、![]() 為函數(shù)圖象上的兩點(diǎn),則
為函數(shù)圖象上的兩點(diǎn),則![]() ;④當(dāng)
;④當(dāng)![]() 時(shí)方程
時(shí)方程![]() 有實(shí)數(shù)根,則
有實(shí)數(shù)根,則![]() 的取值范圍是
的取值范圍是![]() .其中正確的結(jié)論的個(gè)數(shù)為( )
.其中正確的結(jié)論的個(gè)數(shù)為( )
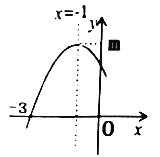
A.1個(gè)B.2個(gè)C.3個(gè)D.4個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,將△ABC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)90°得到△EDC.若點(diǎn)A,D,E在同一條直線上,∠ACB=20°,則∠ADC的度數(shù)是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在水果銷售旺季,某水果店購進(jìn)一優(yōu)質(zhì)水果,進(jìn)價(jià)為20元/千克,售價(jià)不低于20元/千克,且不超過32元/千克,根據(jù)銷售情況,發(fā)現(xiàn)該水果一天的銷售量y(千克)與該天的售價(jià)x(元/千克)滿足如下表所示的一次函數(shù)關(guān)系.
銷售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售價(jià)x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天這種水果的售價(jià)為23.5元/千克,求當(dāng)天該水果的銷售量.
(2)如果某天銷售這種水果獲利150元,那么該天水果的售價(jià)為多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若拋物線![]() (
(![]() 是常數(shù),
是常數(shù),![]() )與直線
)與直線![]() 都經(jīng)過
都經(jīng)過![]() 軸上的一點(diǎn)
軸上的一點(diǎn)![]() ,且拋物線
,且拋物線![]() 的頂點(diǎn)
的頂點(diǎn)![]() 在直線
在直線![]() 上,則稱此直線
上,則稱此直線![]() 與該拋物線
與該拋物線![]() 具有“一帶一路”關(guān)系.此時(shí),直線
具有“一帶一路”關(guān)系.此時(shí),直線![]() 叫做拋物線
叫做拋物線![]() 的“帶線”,拋物線
的“帶線”,拋物線![]() 叫做直線
叫做直線![]() 的“路線”.
的“路線”.
(1)若直線![]() 與拋物線
與拋物線![]() 具有“一帶一路”關(guān)系,求
具有“一帶一路”關(guān)系,求![]() 的值;
的值;
(2)若某“路線”![]() 的頂點(diǎn)在反比例函數(shù)
的頂點(diǎn)在反比例函數(shù)![]() 的圖象上,它的“帶線”
的圖象上,它的“帶線”![]() 的解析式為
的解析式為![]() ,求此“路線”
,求此“路線”![]() 的解析式;
的解析式;
(3)當(dāng)常數(shù)![]() 滿足
滿足![]() 時(shí),請(qǐng)直接寫出拋物線
時(shí),請(qǐng)直接寫出拋物線![]() :
:![]() 的“帶線”
的“帶線”![]() 與
與![]() 軸,
軸,![]() 軸所圍成的三角形面積S的取值范圍.
軸所圍成的三角形面積S的取值范圍.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com