Question

閱讀下列材料：

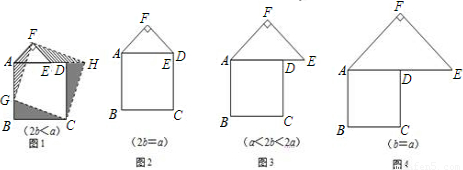
在圖1中，正方形ABCD的邊長為a，等腰直角三角形FAE的斜邊AE＝2b，且邊AD和AE在同一直線上．

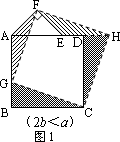
小明的做法：當2b＜a時，如圖1，在BA上選取點G，使BG＝b，連結FG和CG，裁掉△FAG和△CGB并分別拼接到△FEH和△CHD的位置構成四邊形FGCH．

小明在操作后發現：該剪拼方法就是先將△FAG繞點F逆時針旋轉90°到△FEH的位置，易知EH與AD在同一直線上．連結CH，由剪拼方法可得DH＝BG，故△CHD≌△CGB，從而又可將△CGB繞點C順時針旋轉90°到△CHD的位置．這樣，對于剪拼得到的四邊形FGCH(如圖1)，過點F作FM⊥AE于點M(圖略)，利用SAS公理可判斷△HFM≌△CHD，易得FH＝HC＝GC＝FG，∠FHC＝90°．

進而根據正方形的判定方法，可以判斷出四邊形FGCH是正方形．

解決下列問題：

(1)正方形FGCH的面積是________；(用含a，b的式子表示)

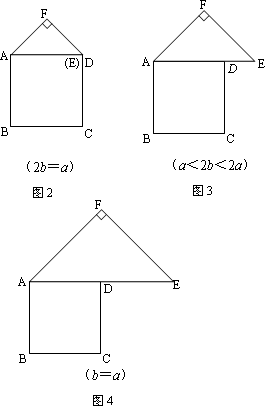
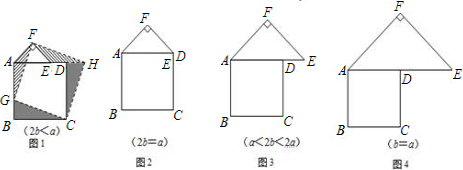
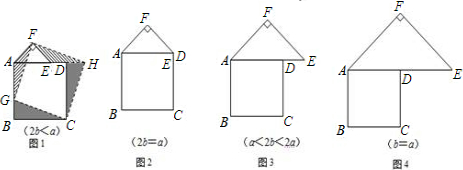
(2)類比圖1的剪拼方法，請你就圖2的三種情形分別畫出剪拼成一個新正方形的示意圖．

Answer 1

答案：
解析：

　　解：(1)a²＋b²　　1分

　　(2)剪拼方法(每圖1分)