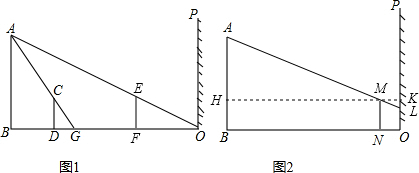
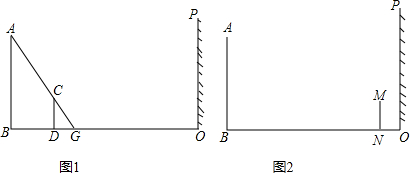
解:(1)∵BO=20米,OD=17米,
∴BD=BO-OD=20-17=3米,
∵DG=1米,
∴BG=BD+DG=3+1=4米,
∵AB、CD都與地面BO垂直,
∴△QBG∽△CDG,
∴

=
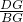
,
即
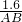
=

,
解得AB=6.4米;
(2)小亮EF的位置如圖所示,
此時,∵△ABO∽△EFO,
∴

=
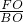
,
即
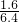
=
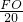
,
解得FO=5米;
(3)如圖,∵小亮距離墻2米,
∴ON=MK=2米,
HM=20-2=18米,
∵AB=6.4米,MN=1,6米,
∴AH=6.4-1.6=4.8米,
∵△AHM∽△LKM,
∴
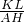
=
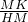
,
即
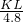
=
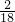
,
解得KL=
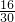
米,
∴在墻上的影子為1.6-
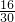
=
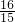
米.
分析:(1)求出BD的長,再求出BG的長,然后根據△QBG和△CDG相似,利用相似三角形對應邊成比例列式求解即可;
(2)根據△ABO和△EFO相似,利用相似三角形對應邊成比例列式求解即可得到影長FO;
(3)設影子在墻上的落點為L,過M作HK∥BO交AB于H,交PO于K,求出AH、HM的長,然后根據△AHM和△LKM相似,利用相似三角形對應邊成比例列式求出KL,再根據MN的長度列式計算即可得解.
點評:本題考查了相似三角形在測量高度時的應用,解題時關鍵是找出相似的三角形,然后根據對應邊成比例列出方程,建立適當的數學模型來解決問題.


 =
=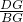 ,
,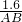 =
= ,
, =
=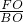 ,
,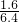 =
=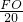 ,
,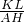 =
=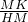 ,
,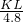 =
=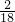 ,
,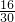 米,
米,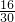 =
=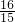 米.
米.

