
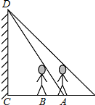
【題目】墻壁![]() 處有一盞燈(如圖),小明站在
處有一盞燈(如圖),小明站在![]() 處測得他的影長與身長相等都為
處測得他的影長與身長相等都為![]() ,小明向墻壁走
,小明向墻壁走![]() 到
到![]() 處發現影子剛好落在A
處發現影子剛好落在A![]() 點,則燈泡與地面的距離
點,則燈泡與地面的距離![]() ________.
________.
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知線段a,P為線段a上任意一點,已知圖形M,Q為圖形M上任意一點,當P,Q兩點間的距離最小時,將此時PQ的長度稱為圖形M與線段a的近點距;當P,Q兩點間的距離最大時,將此時PQ的長度稱為圖形M與線段a的遠點距.

根據閱讀材料解決下列問題:
如圖1,在平面直角坐標系xOy中,點A的坐標為(﹣2,﹣2),正方形ABCD的對稱中心為原點O.
(1)線段AB與線段CD的近點距是 ,遠點距是 .
(2)如圖2,直線y=﹣x+6與x軸,y軸分別交于點E,F,則線段EF和正方形ABCD的近點距是 ,遠點距是 ;
(3)直線y=x+b(b≠0)與x軸,y軸分別交于點R,S,線段RS與正方形ABCD的近距點是![]() ,則b的值是 ;
,則b的值是 ;
(4)在平面直角坐標系xOy中,有一個矩形GHMN,若此矩形至少有一個頂點在以O為圓心1為半徑的圓上,其余各點可能在圓上或圓內,將正方形ABCD繞點O旋轉一周,在旋轉過程中,它與矩形GHMN的近點距的最小值是 ,遠點距的最大值是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
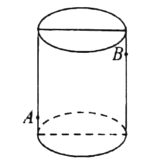
【題目】有一個圓柱形玻璃杯高![]() ,底面周長為
,底面周長為![]() ,有一只螞蟻在一側距下底
,有一只螞蟻在一側距下底![]() 的外側
的外側![]() 點,與點
點,與點![]() 正對的容器內側距下底
正對的容器內側距下底![]() 的
的![]() 點處有一飯粒,螞蟻想吃
點處有一飯粒,螞蟻想吃![]() 處的飯粒,要從杯子的外側爬到杯子的內側,杯子的厚度忽略不計,則至少需要爬________________
處的飯粒,要從杯子的外側爬到杯子的內側,杯子的厚度忽略不計,則至少需要爬________________![]() 。
。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:正方形![]() 中,
中,![]() ,
,![]() 繞點
繞點![]() 順時針旋轉,它的兩邊分別交
順時針旋轉,它的兩邊分別交![]() ,
,![]() (或它們的延長線)于點
(或它們的延長線)于點![]() ,
,![]() 。當
。當![]() 繞點
繞點![]() 旋轉到
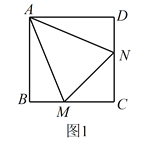
旋轉到![]() 時(如圖1),易證
時(如圖1),易證![]() .(不必證明)
.(不必證明)
(1)當![]() 繞點
繞點![]() 旋轉到
旋轉到![]() 時(如圖2),線段
時(如圖2),線段![]() ,
,![]() 和
和![]() 之間有怎樣的數量關系?寫出猜想,并加以證明。
之間有怎樣的數量關系?寫出猜想,并加以證明。
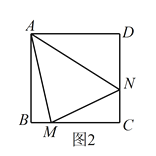
(2)當![]() 繞點
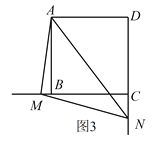
繞點![]() 旋轉到如圖3的位置時,線段
旋轉到如圖3的位置時,線段![]() ,
,![]() 和
和![]() 之間又有怎樣的數量關系?寫出猜想,并加以證明。
之間又有怎樣的數量關系?寫出猜想,并加以證明。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別為
分別為![]() ,
,![]() 上一點,
上一點,![]() ,連接
,連接![]() ,
,![]() ,
,![]() .
.
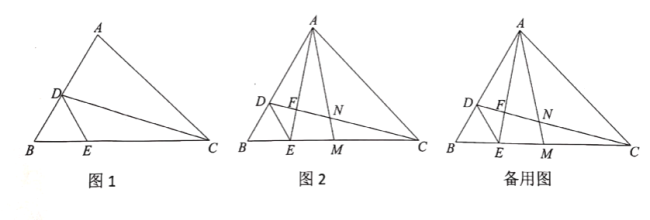
(1)如圖1,若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(2)如圖2,連接![]() 交
交![]() 于點
于點![]() ,點
,點![]() 為
為![]() 上一點,連接
上一點,連接![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,求證:
,求證:![]() ;
;
(3)在(2)的條件下,若![]() ,直接寫出線段
,直接寫出線段![]() ,
,![]() ,
,![]() 的等量關系.
的等量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有甲、乙兩個不透明的布袋,甲袋中有2個完全相同的小球,分別標有數字0和-2;乙袋中有3個完全相同的小球,分別標有數字-2,0和1,小明從甲袋中隨機取出1個小球,記錄標有的數字為x,再從乙袋中隨機取出1個小球,記錄標有的數字為y,這樣確定了點Q的坐標(x,y).
(1)寫出點Q所有可能的坐標;
(2)求點Q在x軸上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),一架云梯AB斜靠在一豎直的墻上,云梯的頂端A距地面15米,梯子的長度比梯子底端B離墻的距離大5米.
(1)這個云梯的底端B離墻多遠?
(2)如圖(2),如果梯子的頂端下滑了8m(AC的長),那么梯子的底部在水平方向右滑動了多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F.
(1)求證:△CBE≌△CDF;
(2)若AB=3,DF=2,求AF的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com