
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別為
分別為![]() ,
,![]() 上一點,
上一點,![]() ,連接
,連接![]() ,
,![]() ,
,![]() .
.
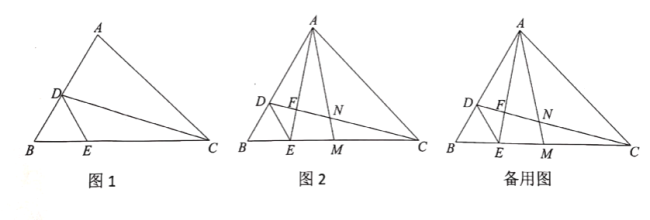
(1)如圖1,若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(2)如圖2,連接![]() 交
交![]() 于點
于點![]() ,點
,點![]() 為
為![]() 上一點,連接
上一點,連接![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,求證:
,求證:![]() ;
;
(3)在(2)的條件下,若![]() ,直接寫出線段
,直接寫出線段![]() ,
,![]() ,
,![]() 的等量關系.
的等量關系.
【答案】(1)9-![]() (2)見解析(3)AD+MC= AC,理由見解析.
(2)見解析(3)AD+MC= AC,理由見解析.
【解析】
(1)過點D作DF⊥BE,根據等邊三角形的的性質求出DF的長,再利用勾股定理求出CF,即可求出EC的長;
(2)作AG=AB, 得到△ABG為等邊三角形,先證明△ABE≌△AGM,再證明△AGC≌△CED,得到CG=DE,再根據MG=BE=DE即可求解;
(3)作AH⊥BC,根據∠ACB=45°,∠BAC=75°,得到∠BAH=30°,∠HAC=45°設BH=x,
根據含30°的直角三角形與等腰直角三角形的性質分別表示出AD,MC,AC,即可求解.
(1)∵![]() ,
,![]() =
=![]()
∴△BDE為等邊三角形,
作DF⊥BE,
∴EF=![]() BE=
BE=![]()
∴DF=![]()
∵CD=![]()
∴CF=![]() =9
=9
∴EC=CF-EF=9-![]() ;
;
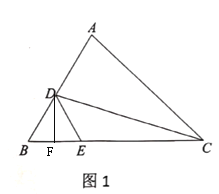
(2)作AG=AB,∵∠B=60°,
∴△ABG為等邊三角形,
∵AE=AM,∠ABE=∠AGM=60°,
∴△ABE≌△AGM,
∴∠ADC=60°+∠2=∠DAC=60°+∠1
故∠1=∠2,
∵∠AGC=120°=∠CED,AC=CD
∴△AGC≌△CED,
∴CG=DE,
又MG=BE=DE,
∴MC=MG+CG=2DE.
(3)∵∠ACB=45°,∠BAC=75°,
∴∠1=∠2=15°,
作AH⊥BC,∴∠BAH=30°,∠HAC=45°
設BH=x,
∴AB=2x,AH=![]() x=CH
x=CH
∴AC=![]() =
=![]() x,BC=(
x,BC=(![]() +1)x,
+1)x,
故CG=BC-BG=(![]() -1)x,BD=CG=(
-1)x,BD=CG=(![]() -1)x
-1)x
AD=AB-BD=(3-![]() )x
)x
CM=(2![]() -x)x
-x)x
∴AD+MC=(![]() +1)x=AC
+1)x=AC
即AD+MC= AC.


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩人在直線跑道上同起點、同終點、同方向勻速跑500米,先到終點的人原地休息.已知甲先出發2秒,在跑步過程中,甲.乙兩人的距離y(米)與乙出發的時間t(秒)之間的關系如圖所示,給出以下結論:①100秒時乙到達終點;②a=8;③b=92④c=125,其中正確的是( )

A.②③B.①②③C.②③④D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國慶期間,魯能巴蜀中學團委決定組織同學們觀看電影《我和我的祖國》,《中國機長》和《攀登者》,小明準備到電影院提前購票.已知三部電影單價之和為100元,計劃購買三部電影票總共不超過135張;其中《攀登者》票價為30元,計劃購買35張,《中國機長》至少購買25張,《我和我的祖國》數量不少于《中國機長》的2倍粗心的小明在做預算時將《我和我的祖國》和《中國機長》的票價弄反了,結果實際購買三種電影票時的總價比預算多了112元,若三部電影票的單價均為整數,則小明實際購買這三部電影票最多需要花費_____元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校對初2021級甲、乙兩班各60名學生進行知識測試(滿分60分),測試完成后分別抽取了12份成績,整理分析過程如下,請補充完整.
(收集數據)
甲班12名學生測試成績統計如下:
45,59,60,38,57,53,52,58,60,50,43,49
乙班12名學生測試成績統計如下:
35,55,46,39,54,47,43,57,42,59,60,47
(整理數據)
按如下分數段整理,描述這兩組樣本數據
組別頻數 |
|
|
|
|
|
甲 | 0 | 1 | 3 | 3 | 5 |
乙 | 2 | 2 | 3 | 1 | 4 |
(分析數據)
兩組樣本數據的平均數、眾數、中位數、方差如下表所示:
班級 | 平均數 | 眾數 | 中位數 |
甲 |
| 52.5 | |
乙 | 48.7 | 47 |
|
(1)![]() ,
,![]() ;
;
(2)若規定得分在40分及以上為合格,請估計乙班60名學生中知識測試合格的學生有多少人?
(3)你認為哪個班的學生知識測試的整體水平較好,請說明一條理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小兒是同班同學,被分到了同一個學習小組,在一次數學活動課上,他們各自用一張面積為![]() 的正方形紙片制作了一副七巧板,合作完成了如圖所示的作品.請計算圖中打圈部分的面積是( )
的正方形紙片制作了一副七巧板,合作完成了如圖所示的作品.請計算圖中打圈部分的面積是( )
少壯不努力,老大徒傷悲
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,已知點
,已知點![]() .
.
(1)求出點![]() ,點
,點![]() 的坐標.
的坐標.
(2)![]() 是直線
是直線![]() 上一動點,且
上一動點,且![]() 和
和![]() 的面積相等,求點
的面積相等,求點![]() 坐標.
坐標.
(3)如圖2,平移直線![]() ,分別交
,分別交![]() 軸,
軸,![]() 軸于交于點
軸于交于點![]() ,
,![]() ,過點
,過點![]() 作平行于
作平行于![]() 軸的直線
軸的直線![]() ,在直線
,在直線![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 是等腰直角三角形?若存在,請直接寫出所有符合條件的點
是等腰直角三角形?若存在,請直接寫出所有符合條件的點![]() 的坐標.
的坐標.
圖1 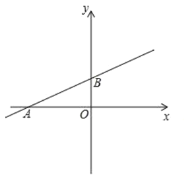 圖2
圖2 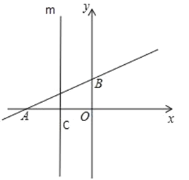
查看答案和解析>>
科目:初中數學 來源: 題型:
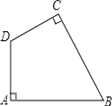
【題目】如圖,在四邊形ABCD中,∠A=∠C=90°.
(1)用直尺和圓規作⊙O,使它經過A、B、D三點(保留作圖痕跡);
(2)點C是否在⊙O上?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
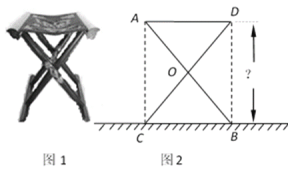
【題目】某大學計劃為新生配備如圖1所示的折疊椅.圖2中的正方形ACBD是折疊椅撐開后的側面示意圖,其中椅腿AB和CD的長相等,O是它們的中點.若正方形ACBD的面積為[9(2x-3y)2+12(2x-3y) (x+4y) +4(x+4y)2](米2)(x>y),你能求出這種折疊椅張開后的高度嗎?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com