【題目】2019年甘肅在國際知名旅游指南《孤獨星球》亞洲最佳旅游地排名第一，截至2020年1月，甘肅省已有五家國家5A級旅游景區，分別為A：嘉峪關文物景區；B：平涼崆峒山風景名勝區；C：天水麥積山景區；D：敦煌鳴沙月牙泉景區：E：張掖七彩舟霞景區，張帆同學與父母計劃在暑假期間從中選擇部分景區游玩．
（1）張帆一家選擇E：張掖七彩丹霞景區的概率是多少？
（2）若張帆一家選擇了E：張掖七彩丹霞景區，他們再從
，
，
，
四個景區中任選兩個景區去旅游，求選，兩個景區的概率（要求畫樹狀圖或列表求概率）．
科目：初中數學 來源： 題型：
【題目】從2018年12月初開始，某地環保部門連續一年對
兩市的空氣質量進行監測，將
天的空氣污染指數(簡稱：API)的平均值作為每個月的空氣污染指數，
個月的空氣污染指數如下：
整理、描述數據：
空氣質量
按如表整理、描述這兩市空氣污染指數的數據：
城市 | 空氣質量為優 | 空氣質量為良 | 空氣質量為輕微污染 |
|
|
|
|
|
說明：空氣污染指數
時，空氣質量為優；
空氣污染指數
時，空氣質量為良；
空氣污染指數
時，空氣質量為輕微污染．
分析數據：
兩市的空氣污染指數的平均數、中位數、眾數如下表所示；
城市 | 平均數 | 中位數 | 眾數 |
|
|
| |
|
|
|
請將以上兩個表格補充完整：
得出結論：可以推斷出 市這一年中環境狀況比較好，理由_____．(至少從兩個不同的角度說明推斷的合理性)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“2020第二屆貴陽市應急科普知識大賽”的比賽中有一個抽獎活動．規則是：準備3張大小一樣，背面完全相同的卡片，3張卡片的正面所寫內容分別是《消防知識手冊》《辭海》《辭海》，將它們背面朝上洗勻后任意抽出一張，抽到卡片后可以免費領取卡片上相應的書籍．
（1）在上面的活動中，如果從中隨機抽出一張卡片，記下內容后不放回，再隨機抽出一張卡片，請用列表或畫樹狀圖的方法，求恰好抽到2張卡片都是《辭海》的概率；
（2）再添加幾張和原來一樣的《消防知識手冊》卡片，將所有卡片背面朝上洗勻后，任意抽出一張，使得抽到《消防知識手冊》卡片的概率為
，那么應添加多少張《消防知識手冊》卡片？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了豐富學生們的課余生活，學校準備開展第二課堂，有四類課程可供選擇，分別是“A．書畫類、B．文藝類、C．社會實踐類、D．體育類”．現隨機抽取了七年級部分學生對報名意向進行調查，并根據調查結果繪制了兩幅不完整的統計圖，請你根據圖表信息回答下列問題：
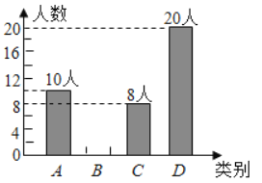
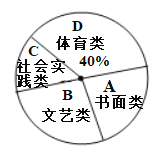
（1）本次被抽查的學生共有_____________名，扇形統計圖中“A．書畫類”所占扇形的圓心角的度數為___________度；
（2）請你將條形統計圖補全；
（3）若該校七年級共有600名學生，請根據上述調查結果估計該校學生選擇“C．社會實踐類”的學生共有多少名？
（4）本次調查中抽中了七（1）班王芳和小穎兩名學生，請用列表法或畫樹狀圖法求她們選擇同一個項目的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
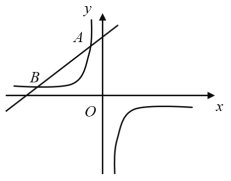
【題目】如圖，一次函數
的圖象與反比例函數
（
為常數且
）的圖象相交于
，
兩點．
（1）求反比例函數的表達式；
（2）將一次函數的圖象沿
軸向下平移
個單位
，使平移后的圖象與反比例函數的圖象有且只有一個交點，求的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
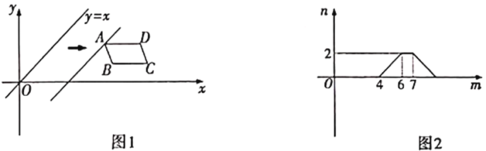
【題目】如圖1，在平面直角坐標系中，
在第一象限，且
軸．直線
從原點
出發沿
軸正方向平移．在平移過程中，直線被截得的線段長度
與直線在軸上平移的距離
的函數圖象如圖2所示．那么的面積為（ ）
A.3B.
C.6D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】黃河是中華民族的象征，被譽為母親河，黃河壺口瀑布位于我省吉縣城西45千米處，是黃河上最具氣勢的自然景觀．其落差約30米，年平均流量1010立方米/秒．若以小時作時間單位，則其年平均流量可用科學記數法表示為（ ）
A. 6.06×104立方米/時 B. 3.136×106立方米/時
C. 3.636×106立方米/時 D. 36.36×105立方米/時
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，已知直線AB的函數解析式為y=﹣2x+8，與x軸交于點A，與y軸交于點B．
（1）求A、B兩點的坐標；
（2）若點P（m，n）為線段AB上的一個動點（與A、B不重合），作PE⊥x軸于點E，PF⊥y軸于點F，連接EF，問：
①若△PAO的面積為S，求S關于m的函數關系式，并寫出m的取值范圍；
②是否存在點P，使EF的值最小？若存在，求出EF的最小值；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
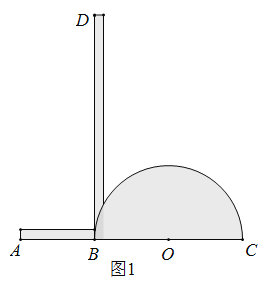
【題目】我們學習過利用用尺規作圖平分一個任意角，而“利用尺規作圖三等分一個任意角”曾是數學史上一大難題，之后被數學家證明是不可能完成的，人們根據實際需要，發明了一種簡易操作工具--------三分角器．圖1是它的示意圖，其中
與半圓
的直徑
在同一直線 上，且的長度與半圓的半徑相等；
與
重直于點 
足夠長．
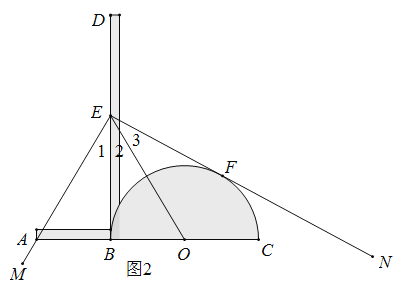
使用方法如圖2所示，若要把
三等分，只需適當放置三分角器，使經過的頂點
，點
落在邊
上，半圓與另一邊
恰好相切，切點為
，則
就把三等分了．
為了說明這一方法的正確性，需要對其進行證明．如下給出了不完整的“已知”和“求證”，請補充完整，并寫出“證明”過程．
已知：如圖2，點在
同一直線上，
垂足為點
，
求證：
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
