已知Rt△ABC的兩直角邊AC=5,BC=12,D是BC上一點.當(dāng)AD是∠A的平分線時,則CD= .
【答案】
分析:由題意畫出相應(yīng)的圖形,過D作DE于AB垂直,垂足為E,由AD為角平分線,利用角平分線定理得到DC=DE,再由AD為公共邊,利用HL可得直角三角形ADC與直角三角形ADE全等,根據(jù)全等三角形對應(yīng)邊相等可得AE=AC,在直角三角形ABC中,由AC及BC的長,利用勾股定理求出AB的長,再由BE=AB-AE=AB-AC,求出BE的長,設(shè)CD=DE=x,則有DB=BC-x=12-x,在直角三角形DEB中,利用勾股定理列出關(guān)于x的方程,求出方程的解得到x的值,進而得到CD的長.
解答: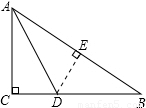
解:根據(jù)題意作出相應(yīng)的圖形,如圖所示,
過點E作ED⊥AB,交AB于點E,
∵AD為∠A的平分線,ED⊥AB,DC⊥AC,
∴DC=DE,
在Rt△ACD和Rt△AED中,
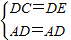
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=5,
在Rt△ABC中,由AC=5,BC=12,
根據(jù)勾股定理得:AB=
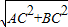
=13,
∴EB=AB-AE=AB-AC=13-5=8,
設(shè)CD=DE=x,BD=12-x,
在Rt△BDE中,利用勾股定理得:DE
2+EB
2=DB
2,
即x
2+8
2=(12-x)
2,解得x=
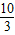
,
則CD=
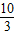
.
故答案為:
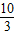
.
點評:此題考查了角平分線的性質(zhì),全等三角形的判定與性質(zhì),以及勾股定理的應(yīng)用,在出現(xiàn)角平分線時,常常過角平分線上一點作角兩邊的垂線,利用角平分線上的點到角兩邊的距離相等來解決問題.根據(jù)題意畫出圖形,利用勾股定理列出相應(yīng)的方程是解本題的關(guān)鍵.

 解:根據(jù)題意作出相應(yīng)的圖形,如圖所示,
解:根據(jù)題意作出相應(yīng)的圖形,如圖所示,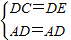 ,
,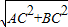 =13,
=13,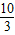 ,
,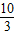 .
.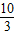 .
.
