
【題目】閱讀下面材料:小明遇到這樣一個問題:
如圖1,在△ABC中,∠B=2∠C,AD⊥BC于點D,求證:BC=AB+2BD.
小明利用條件AD⊥BC,在CD上截取DH=BD,如圖2,連接AH,既構造了等腰△ABH,又得到BH=2BD,從而命題得證。
(1)根據閱讀材料,證明:BC=AB+2BD;
(2)參考小明的方法,解決下面的問題:
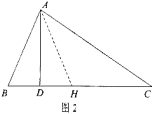
如圖3,在△ABC中,∠BAC=90°,∠ABD=∠BCE,∠ABC=∠DCE,請探究AD與BE的數量關系,并說明理由。


【答案】(1)證明見解析;(2)BE=2AD.
【解析】
(1)由BD=DH,AD⊥BH,得到AB=AH,由等邊對等角得到∠B=∠AHB,再由∠B=2∠C和三角形外角的性質得到∠C=∠CAH,由等角對等邊得到AH=HC,即有AB=HC,從而可以得出結論;
(2)延長DA至點F,使得AF=AD,連接BF.設∠ABD=∠BCE=x,∠ABC=∠DCE=y.
證明BA垂直平分DF,得到BF=BD,∠1=∠DBA=x,進而得到∠FBC=∠ACB,由等角對等邊得到BF=CF,即有BD=FC.由三角形外角的性質得到∠2=∠DCE,則有DE=DC,結合BD=CF,即可得到結論.
(1)∵BD=DH,AD⊥BH,∴AB=AH,∴∠B=∠AHB.
∵∠B=2∠C,∴∠AHB=2∠C=∠C+∠CAH,∴∠C=∠CAH,∴AH=HC,∴AB=HC,∴BC=HC+BH=AB+2BD.
(2)BE=2AD.理由如下:
延長DA至點F,使得AF=AD,連接BF.設∠ABD=∠BCE=x,∠ABC=∠DCE=y.
∵AF=AD,∠BAD=90°,∴BA垂直平分DF,∴BF=BD,∠1=∠DBA=x,∴∠FBC=∠1+∠ABC=x+y,∠ACB=∠DCE+∠ECB=x+y,∴∠FBC=∠ACB,∴BF=CF.
∵BF=BD,∴BD=FC.
∵∠2=∠3+x=∠ABC=y=∠DCE,∴DE=DC.
∵BD=FC,∴BE+DE=2AD+DC,∴BE=2AD.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
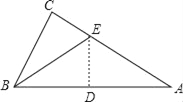
【題目】有一直角三角形紙片,∠C=90°,BC=6,AC=8,現將△ABC按如圖那樣折疊,使點A與點B重合,折痕為DE,則CE的長為( )
A. 2![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若將一幅三角板按如圖所示的方式放置,則下列結論中不正確的是( )

A. ∠1=∠3 B. 如果∠2=30°,則有AC∥DE
C. 如果∠2=30°,則有BC∥AD D. 如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學期結束前,學校想調查七年級學生對新課改實驗教材的意見,特向七年級480名學生作了問卷調查,結果如下表所示:
意見 | 非常喜歡 | 喜歡 | 有一點喜歡 | 不喜歡 |
人數 | 240 | 192 | 44 | 4 |
(1)計算出每一種意見的人數占調查總人數的百分比;
(2)請作出反映此調查結果的扇形統計圖;
(3)從統計圖中你能得出什么結論?說說你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
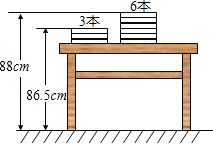
【題目】如圖,兩摞規格完全相同的課本整齊疊放在講臺上請根據圖中所給出的數據信息,回答下列問題:
(1)每本課本的厚度為______cm;
(2)若有一摞上述規格的課本x本,整齊疊放在講臺上,請用含x的代數式表示出這一摞數學課本的頂部距離地面的高度為______cm;
(3)當x=48時,若從中取走10本,求余下的課本的頂部距離地面的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
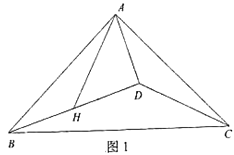
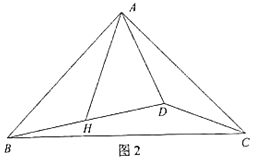
【題目】已知等腰Rt△ABC,∠BAC=90°,AB=AC,點D為△ABC內部一點,連接AD、BD、CD,點H為BD中點,連接AH,且∠BAH=∠ACD.
(1)如圖1,若∠ADB=90°,求證:∠DAH=45°;
(2)如圖2,若∠ADB<90°,(1)問中的結論是否成立,若成立,請證明;若不成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
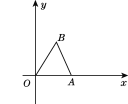
【題目】如圖,在直角坐標系中,已知點A(6,0),又點B(x,y)在第一象限內,且x+y=8,設△AOB的面積是S.
(1)寫出S與x之間的函數解析式,并求出x的取值范圍;
(2)畫出(1)中所求函數的圖象.
查看答案和解析>>
科目:初中數學 來源: 題型:
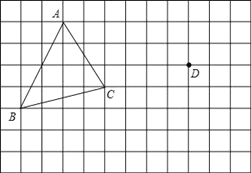
【題目】在正方形網格中,每個小正方形的邊長均為1個單位長度,△ABC的三個頂點的位置如圖所示.現將△ABC平移,使點A變換為點D,點E、F分別是B、C的對應點.
(1)請畫出平移后的△DEF.
(2)若連接AD、CF,則這兩條線段之間的關系是 .
(3)畫出△ABC的BC邊上的高AM。
(4)滿足三角形ACP的面積等于三角形ACB的面積的格點P有 個(不和B重合)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A、B兩點,與y軸交于點C,對稱軸為直線x=﹣1,點B的坐標為(1,0),則下列結論:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正確的結論有( )個.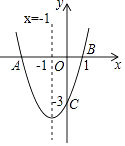
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com