
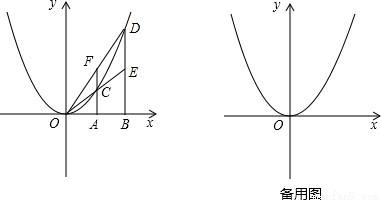
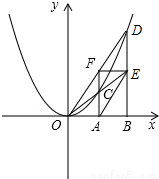
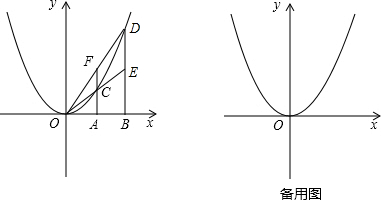
 (2)綜合上面的結論,可得出E、F的縱坐標相同,即EF∥x軸,則四邊形ABEF是矩形;
(2)綜合上面的結論,可得出E、F的縱坐標相同,即EF∥x軸,則四邊形ABEF是矩形; (FE+OB)•BE=3×
(FE+OB)•BE=3× FE•BE,
FE•BE,

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

 (k>0)的圖象上,過點M作ME⊥y軸,過點N作NF⊥x軸,垂足分別為E、F.你發現MN與EF之間有著怎樣的位置關系?說明你的理由.
(k>0)的圖象上,過點M作ME⊥y軸,過點N作NF⊥x軸,垂足分別為E、F.你發現MN與EF之間有著怎樣的位置關系?說明你的理由. (x>0,m是不為0的常數)的圖象經過點A(1,4)、B(a,b),其中a>1.過點A作x軸的垂線,垂足為C,過點B作y軸的垂線,垂足為D,AC與BD相交于點M,連接AD、DC、CB與AB.已知AD=BC,求直線AB的函數關系式.
(x>0,m是不為0的常數)的圖象經過點A(1,4)、B(a,b),其中a>1.過點A作x軸的垂線,垂足為C,過點B作y軸的垂線,垂足為D,AC與BD相交于點M,連接AD、DC、CB與AB.已知AD=BC,求直線AB的函數關系式.查看答案和解析>>
科目:初中數學 來源: 題型:
問題情境
如圖,在![]() 軸上有兩點
軸上有兩點![]() ,
,![]() (
(![]() ).分別過點
).分別過點![]() ,點
,點![]() 作
作![]() 軸的垂線,交拋物線
軸的垂線,交拋物線![]() 于點
于點![]() 、點
、點![]() .直線
.直線![]() 交直線
交直線![]() 于點
于點![]() ,直線
,直線![]() 交直線
交直線![]() 于點
于點![]() ,點
,點![]() 、點
、點![]() 的縱坐標分別記為
的縱坐標分別記為![]() 、
、![]() .
.
![]()

特例探究
填空:
當![]() ,
,![]()
![]() 時,
時,![]() =____,
=____,![]() =______.當
=______.當![]() ,
,![]() 時,
時,![]() =____,
=____,![]() =______.
=______.
歸納證明
對任意![]() ,
,![]() (
(![]() ),猜想
),猜想![]() 與
與![]() 的大小關系,并證明你的猜想
的大小關系,并證明你的猜想
拓展應用.
(1) 若將“拋物線![]() ”改為“拋物線
”改為“拋物線![]() ”,其它條件不變,請直接寫出
”,其它條件不變,請直接寫出![]() 與
與![]() 的大小關系.
的大小關系.
(2) 連接![]() ,
,![]() .當
.當![]() 時,直接寫出
時,直接寫出![]() 和
和![]() 的關系及四邊形
的關系及四邊形![]() 的形狀.
的形狀.
 [
[
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com