
問題情境
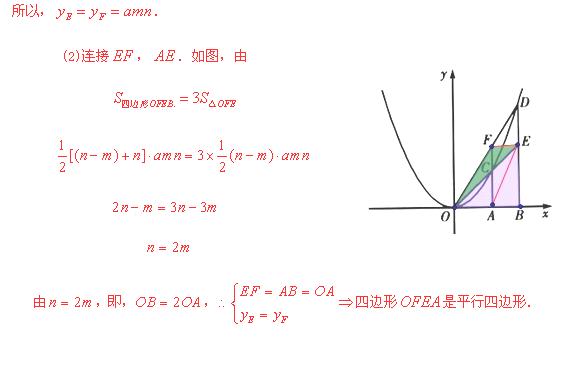
如圖,在![]() 軸上有兩點
軸上有兩點![]() ,
,![]() (
(![]() ).分別過點
).分別過點![]() ,點
,點![]() 作
作![]() 軸的垂線,交拋物線
軸的垂線,交拋物線![]() 于點
于點![]() 、點
、點![]() .直線
.直線![]() 交直線
交直線![]() 于點
于點![]() ,直線
,直線![]() 交直線
交直線![]() 于點
于點![]() ,點
,點![]() 、點
、點![]() 的縱坐標分別記為
的縱坐標分別記為![]() 、
、![]() .
.
![]()

特例探究
填空:
當![]() ,
,![]()
![]() 時,
時,![]() =____,
=____,![]() =______.當
=______.當![]() ,
,![]() 時,
時,![]() =____,
=____,![]() =______.
=______.
歸納證明
對任意![]() ,
,![]() (
(![]() ),猜想
),猜想![]() 與
與![]() 的大小關系,并證明你的猜想
的大小關系,并證明你的猜想
拓展應用.
(1) 若將“拋物線![]() ”改為“拋物線
”改為“拋物線![]() ”,其它條件不變,請直接寫出
”,其它條件不變,請直接寫出![]() 與
與![]() 的大小關系.
的大小關系.
(2) 連接![]() ,
,![]() .當
.當![]() 時,直接寫出
時,直接寫出![]() 和
和![]() 的關系及四邊形
的關系及四邊形![]() 的形狀.
的形狀.
 [
[
答案] 特例探究![]() ;
;![]() .歸納證明 猜想
.歸納證明 猜想![]() .證明(略)拓展應用(1)
.證明(略)拓展應用(1)![]() .(2)四邊形
.(2)四邊形![]() 是平行四邊形.
是平行四邊形.
[考點] 一次函數、二次函數綜合運用,函數圖象上的點與函數解析式的關系,平行四邊形的判定.
[解析] 特例探究
當![]() ,
,![]() 時,
時,![]() ,
,![]() ,所以直線
,所以直線![]() 的解析式為:
的解析式為:![]() ;直線
;直線![]() 的解析式為:
的解析式為:![]() ;此時
;此時
解![]() ,得
,得![]() .解
.解![]() ,得
,得![]() .
.
所以,此時![]()
當![]() ,
,![]() 時,
時,![]() ,
,![]() ,所以直線
,所以直線![]() 的解析式為:
的解析式為:![]() ;直線
;直線![]() 的解析式為:
的解析式為:![]() ;此時
;此時
解![]() ,得
,得![]() .解
.解![]() ,得
,得![]() .
.
所以,此時![]()
歸納證明 猜想:對任意![]() ,
,![]() (
(![]() ),都有:
),都有:![]() .
.
![]() 證明:對任意
證明:對任意![]() ,
,![]() (
(![]() )時,
)時,![]() ,
,![]() ,所以直線
,所以直線![]() 的解析式為:
的解析式為:![]() ;直
;直![]() 線
線![]() 的解析式為:
的解析式為:![]() ;此時
;此時
解![]() ,得
,得![]() .解
.解![]() ,得
,得![]() .
.
所以,此時![]() .
.
拓展應用
(1)若將“拋物線![]() ”改為“拋物線
”改為“拋物線![]() ”,其它條件不變,仍然有:
”,其它條件不變,仍然有:![]() .
.
此時,![]() ,
,![]() ,所以直線
,所以直線![]() 的解析式為:
的解析式為:![]() ;直線
;直線![]() 的解析式為:
的解析式為:![]() ;此時
;此時
解![]() ,得
,得![]() .解
.解![]() ,得
,得![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
 (2013•天津)如圖,是一對變量滿足的函數關系的圖象,有下列3個不同的問題情境:
(2013•天津)如圖,是一對變量滿足的函數關系的圖象,有下列3個不同的問題情境:查看答案和解析>>
科目:初中數學 來源:2012-2013學年湖北省鄂州市第三中學八年級下學期期中考試數學試卷(帶解析) 題型:解答題
[問題情境] 勾股定理是一條古老的數學定理,它有很多證明方法,我國漢代數學家趙爽根據弦圖利用面積法進行證明,著名數學家華羅庚曾提出把“數形關系”帶到其他星球作為地球人與其他星球“人”進行第一次“談話”的語言。
[定理表述] 請你根據圖(1)中的直角三角形敘述勾股定理(用文字及符號語言敘述);

[嘗試證明] 以圖(1)中的直角三角形為基礎可以構造出以a、b為底,以a+b為高的直角梯形如圖(2)。請你利用圖(2)驗證勾股定理;
[知識拓展] 利用圖(2)的直角梯形,我們可以證明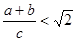 ,其證明步驟如下:
,其證明步驟如下:
∵BC=a+b,AD= .
又∵在直角梯形ABCD中有直角腰BC 斜腰AD(填“>”,“<”或“=”),即 。
∴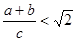
查看答案和解析>>
科目:初中數學 來源:2014屆湖北省鄂州市八年級下學期期中考試數學試卷(解析版) 題型:解答題
[問題情境] 勾股定理是一條古老的數學定理,它有很多證明方法,我國漢代數學家趙爽根據弦圖利用面積法進行證明,著名數學家華羅庚曾提出把“數形關系”帶到其他星球作為地球人與其他星球“人”進行第一次“談話”的語言。
[定理表述] 請你根據圖(1)中的直角三角形敘述勾股定理(用文字及符號語言敘述);
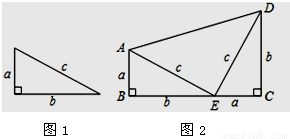
[嘗試證明] 以圖(1)中的直角三角形為基礎可以構造出以a、b為底,以a+b為高的直角梯形如圖(2)。請你利用圖(2)驗證勾股定理;
[知識拓展] 利用圖(2)的直角梯形,我們可以證明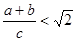 ,其證明步驟如下:
,其證明步驟如下:
∵BC=a+b,AD= .
又∵在直角梯形ABCD中有直角腰BC 斜腰AD(填“>”,“<”或“=”),即 。
∴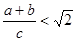
查看答案和解析>>
科目:初中數學 來源: 題型:
情境觀察
將矩形ABCD紙片沿對角線AC剪開,得到△ABC和△A′C′D,如圖1所示.將△A′C′D的頂點A′與點A重合,并繞點A按逆時針方向旋轉,使點D、A(A′)、B在同一條直線上,如圖2所示.
觀察圖2可知:與BC相等的線段是 ,∠CAC′= °.
問題探究
如圖3,△ABC中,AG⊥BC于點G,以A為直角頂點,分別以AB、AC為直角邊,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,過點E、F作射線GA的垂線,垂足分別為P、Q. 試探究EP與FQ之間的數量關系,并證明你的結論.
 | |||
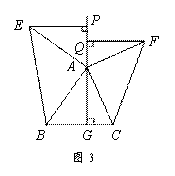 | |||
拓展延伸
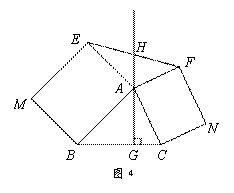
如圖4,△ABC中,AG⊥BC于點G,分別以AB、AC為一邊向△ABC外作矩形ABME和矩形ACNF,射線GA交EF于點H. 若AB= k AE,AC= k AF,試探究HE與HF之間的數量關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com