
【題目】在△ABC中,AB=AC,∠A=60°,點D是BC邊的中點,作射線DE,與邊AB交于點E,射線DE繞點D順時針旋轉120°,與直線AC交于點F.
(1)依題意將圖1補全;
(2)小華通過觀察、實驗提出猜想:在點E運動的過程中,始終有DE=DF.小華把這個猜想與同學們進行交流,通過討論,形成了證明該猜想的幾種想法:
想法1:由點D是BC邊的中點,通過構造一邊的平行線,利用全等三角形,可證DE=DF;
想法2:利用等邊三角形的對稱性,作點E關于線段AD的對稱點P,由∠BAC與∠EDF互補,可得∠AED與∠AFD互補,由等角對等邊,可證DE=DF;
想法3:由等腰三角形三線合一,可得AD是∠BAC的角平分線,由角平分線定理,構造點D到AB,AC的高,利用全等三角形,可證DE=DF…….
請你參考上面的想法,幫助小華證明DE=DF(選一種方法即可);
(3)在點E運動的過程中,直接寫出BE,CF,AB之間的數量關系.
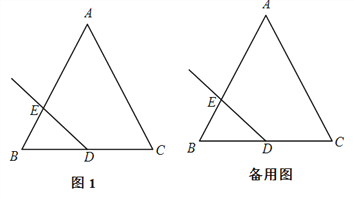
【答案】(1)將圖1補全見解析;
(2)證明見解析;
(3)數量關系:當點F在AC邊上時, ![]() ;
;
當點F在AC延長線上時, ![]() .
.
【解析】試題分析:(1)根據要求畫出圖形即可;(2)選擇一種自己比較熟練的方法進行證明即可;(3)本題分點F在AC邊上,點F在AC延長線上,兩種情況分析即可.
試題解析:解:(1)如圖1,

(2)
想法1證明:如圖2,過D作DG∥AB,交AC于G,
∵點D是BC邊的中點,
∴DG=![]() AB.
AB.
∴△CDG是等邊三角形.
∴∠EDB+∠EDG=120°.
∵∠FDG+∠EDG=120°,
∴∠EDB =∠FDG.
∵BD=DG,∠B=∠FGD=60°,
∴△BDE≌△GDF.
∴DE=DF.
想法2證明:如圖3,連接AD,
∵點D是BC邊的中點,
∴AD是△ABC的對稱軸.
作點E關于線段AD的對稱點P,點P在邊AC上,
∴△ADE≌△ADP.
∴DE=DP,∠AED=∠APD.
∵∠BAC+∠EDF=180°,
∴∠AED+∠AFD=180°.
∵∠APD+∠DPF=180°,
∴∠AFD=∠DPF.
∴DP=DF.
∴DE=DF.
想法3證明:如圖4,連接AD,過D作DM⊥AB于M,DN⊥AB于N,
∵點D是BC邊的中點,
∴AD平分∠BAC.
∵DM⊥AB于M,DN⊥AB于N,
∴DM=DN.
∵∠A=60°,
∴∠MDE+∠EDN=120°.
∵∠FDN+∠EDN=120°,
∴∠MDE=∠FDN.
∴Rt△MDE≌Rt△NDF.
∴DE=DF.
(3)當點F在AC邊上時, ![]() ;
;
當點F在AC延長線上時, ![]() .
.


科目:初中數學 來源: 題型:
【題目】下列說法中,錯誤的有( ).
①一組數據的標準差是它的差的平方;②數據8,9,10,11,1l的眾數是2;③如果數據 ![]() ,
, ![]() ,…,
,…, ![]() 的平均數為
的平均數為 ![]() ,那么
,那么 ![]() ;④數據0,-1,l,-2,1的中位數是l.
;④數據0,-1,l,-2,1的中位數是l.
A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品原價500元,連續兩次降價a%后售價為200元,下列所列方程正確的是( )
A.500(1+a%)2=200
B.500(1-a%)2=200
C.500(1-2a%)=200
D.500(1-a2%)=200
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙丙丁四支足球隊在全國甲級聯賽中進球數分別為:9,9,x , 7,若這組數據的眾數與平均數恰好相等,則這組數據的中位數是( )
A.10
B.9
C.8
D.7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把方程x(x+2)=5(x-2)化成一般式,則a、b、c的值分別是( )
A.1、-3、10
B.1、7、-10
C.1、-5、12
D.1、3、2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列結論中不正確的是( )
A. 平方為9的數是+3或﹣3 B. 立方為27的數是3或﹣3
C. 絕對值為3的數是3或﹣3 D. 倒數等于原數的數是1或﹣1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com