
【題目】已知:如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() (
(![]() )的圖象交于點
)的圖象交于點![]() .
.![]() 軸于點
軸于點![]() ,
,![]() 軸于點
軸于點![]() . 一次函數的圖象分別交
. 一次函數的圖象分別交![]() 軸、
軸、![]() 軸于點
軸于點![]() 、點
、點![]() ,且
,且![]() ,
,![]() .
.
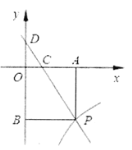
(1)求點![]() 的坐標;
的坐標;
(2)求一次函數與反比例函數的解析式;
(3)根據圖象寫出當![]() 取何值時,一次函數的值小于反比例函數的值?
取何值時,一次函數的值小于反比例函數的值?
【答案】(1)![]() 的坐標為
的坐標為![]() ;(2)
;(2)![]() ,
, ![]() ; (3)當
; (3)當![]() 時,一次函數的值小于反比例函數的值.
時,一次函數的值小于反比例函數的值.
【解析】
(1)本題需先根據題意一次函數與y軸的交點,從而得出D點的坐標.
(2)本題需先根據在Rt△COD和Rt△CAP中,![]() ,OD=3,再根據S△DBP=27,從而得出BP得長和P點的坐標,即可求出結果.
,OD=3,再根據S△DBP=27,從而得出BP得長和P點的坐標,即可求出結果.
(3)根據圖形從而得出x的取值范圍即可.
解:(1)∵一次函數![]() 與
與![]() 軸相交,
軸相交,
∴令![]() ,解得
,解得![]() ,
,
∴![]() 的坐標為
的坐標為![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
∴![]() ,
,
故![]() ,
,
把![]() 坐標代入
坐標代入![]() ,得到
,得到![]() ,
,
則一次函數的解析式為:![]() ;
;
把![]() 坐標代入反比例函數解析式得
坐標代入反比例函數解析式得![]() ,
,
則反比例解析式為:![]() ;
;
(3)如圖:
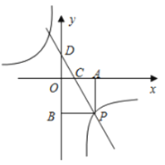
根據圖象可得: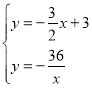 ,
,
解得:![]() 或
或 ![]()
故直線與雙曲線的兩個交點為![]() ,
,![]() ,
,
∵![]() ,
,
∴當![]() 時,一次函數的值小于反比例函數的值.
時,一次函數的值小于反比例函數的值.


 互動課堂系列答案
互動課堂系列答案科目:初中數學 來源: 題型:
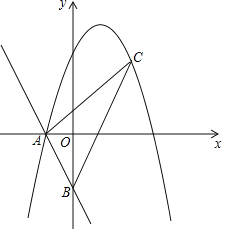
【題目】一次函數y=﹣2x﹣2分別與x軸、y軸交于點A、B.頂點為(1,4)的拋物線經過點A.
(1)求拋物線的解析式;
(2)點C為第一象限拋物線上一動點.設點C的橫坐標為m,△ABC的面積為S.當m為何值時,S的值最大,并求S的最大值;
(3)在(2)的結論下,若點M在y軸上,△ACM為直角三角形,請直接寫出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=AB,把△ABC繞點A順時針旋轉得到△ADE(點B、C分別對應點D、E),BD和CE交于點F.
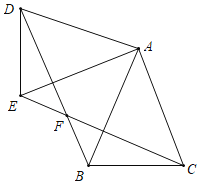
(1)求證:CE=BD;
(2)若AB=2,∠BAC=45°,當四邊形ADFC是平行四邊形時,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小元步行從家去火車站,走到 6 分鐘時,以同樣的速度回家取物品,然后從家乘出租車趕往火車站,結果比預計步行時間提前了3 分鐘.小元離家路程S(米)與時間t(分鐘)之間的函數圖象如圖,從家到火車站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:四邊形 ABCD 內接于⊙O,連接 AC、BD,∠BAD+2∠ACB=180°.
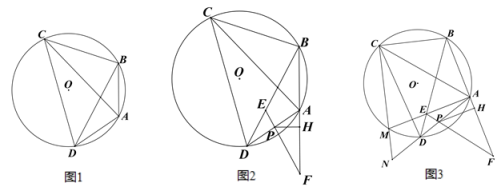
(1)如圖 1,求證:點 A 為弧 BD 的中點;
(2)如圖 2,點 E 為弦 BD 上一點,延長 BA 至點 F,使得 AF=AB,連接 FE 交 AD 于點 P,過點 P 作 PH⊥AF 于點 H,AF=2AH+AP,求證:AH:AB=PE:BE;
(3)在(2)的條件下,如圖 3,連接 AE,并延長 AE 交⊙O 于點 M,連接 CM,并延長 CM 交 AD 的延長線于點 N,連接 FD,∠MND=∠MED,DF=12﹒sin∠ACB,MN=![]() ,求 AH 的長.
,求 AH 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠BAD=80°,AB的垂直平分線交對角線AC于點F,垂足為E,連接DF,則∠CDF等于()
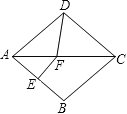
A.50°B.60°C.70°D.80°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖1,拋物線![]() 過
過![]() 三點,頂點為點
三點,頂點為點![]() ,連接
,連接![]() ,點
,點![]() 為拋物線對稱軸上一點,連接
為拋物線對稱軸上一點,連接![]() ,直線
,直線![]() 過點
過點![]() 兩點.
兩點.
(1)求拋物線![]() 及直線
及直線![]() 的函數解析式;
的函數解析式;
(2)求![]() 的最小值;
的最小值;
(3)求證:![]() ∽
∽![]() ;
;
(4)如圖2,若點![]() 是在拋物線
是在拋物線![]() 上且位于第一象限內的一動點,請直接寫出
上且位于第一象限內的一動點,請直接寫出![]() 面積的最大值及此時點
面積的最大值及此時點![]() 的坐標.
的坐標.
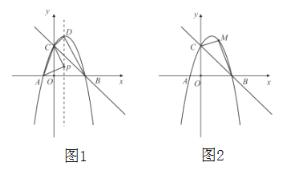
查看答案和解析>>
科目:初中數學 來源: 題型:
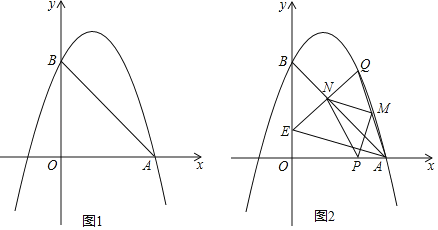
【題目】如圖,拋物線y=﹣x2+bx+c與x軸正半軸交于A點,與y軸正半軸交于B,直線AB的解析式為y=﹣x+3.
(1)求拋物線解析式;
(2)P為線段OA上一點(不與O、A重合),過P作PQ⊥x軸交拋物線于Q,連接AQ,M為AQ中點,連接PM,過M作MN⊥PM交直線AB于N,若點P的橫坐標為t,點N的橫坐標為n,求n與t的函數關系式;
(3)在(2)的條件下,連接QN并延長交y軸于E,連接AE,求t為何值時,MN∥AE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“安全教育平臺”是中國教育學會為方便學長和學生參與安全知識活動、接受安全提醒的一種應用軟件.某校為了了解家長和學生參與“防溺水教育”的情況,在本校學生中隨機抽取部分學生作調查,把收集的數據分為以下4類情形:A.僅學生自己參與;B.家長和學生一起參與;
C.僅家長自己參與; D.家長和學生都未參與.

請根據圖中提供的信息,解答下列問題:
(1)在這次抽樣調查中,共調查了________名學生;
(2)補全條形統計圖,并在扇形統計圖中計算C類所對應扇形的圓心角的度數;
(3)根據抽樣調查結果,估計該校2000名學生中“家長和學生都未參與”的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com