
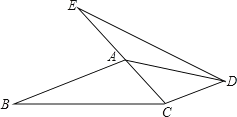
【題目】已知:如圖,點E、A、C在同一條直線上,AB∥CD,AB=CE,∠B=∠E.
(1)求證:△ABC≌△CED;
(2)若∠B=25°,∠ACB=45°,求∠ADE的度數.
【答案】(1)證明見解析,(2)10°.
【解析】試題分析:(1)根據平行線得出∠BAC=∠ECD,結合題目中的已知條件得出三角形全等;(2)根據三角形全等得出CA=CD,即∠CAD=∠CDA,然后根據三角形外角的性質以及角度之間的關系求出答案.
試題解析:(1)∵AB∥CD,∴∠BAC=∠ECD,又∵∠B=∠E,AB=CE,
∴△ABC≌△CED;
(2)∵△ABC≌△CED, ∴∠E=∠B=25°,∠EDC=∠ACB=45°,CA=CD,
∴∠CAD=∠CDA, 設∠ADE=x, 根據外角的性質可知:∠CAD=∠E+∠ADE=25°+x,
∴25°+x=45°-x,解得:x=10°,即∠ADE=10°.


科目:初中數學 來源: 題型:
【題目】某中學規定學生的學期體育成績滿分為100分,其中早鍛煉及體育課外活動占20%,期中考試成績占30%,期末考試成績占50%.小桐的三項成績(百分制)依次為95,90,85.則小桐這學期的體育成績是( )
A. 88.5B. 86.5C. 90D. 90.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】大眾創業,萬眾創新,據不完全統計,2015年畢業的大學生中創業人數已經達到7490000人,將7490000這個數據用科學記數法表示為( )
A.7.49×107
B.7.49×106
C.74.9×106
D.0.749×107
查看答案和解析>>
科目:初中數學 來源: 題型:
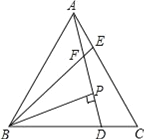
【題目】如圖,已知△ABC為等邊三角形,AE=CD,AD、BE相交于點F.
(1)求證:△ABE≌△CAD;
(2)若BP⊥AD于點P,PF=9,EF=3,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是∠AOB的角平分線OC上一點,分別連接AP、BP,若再添加一個條件即可判定△AOP≌△BPO,則一下條件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正確的是 (只需填序號即可)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班抽取6名同學參加體能測試,成績如下:80,90,75,75,80,80.下列表述錯誤的是( )
A. 眾數是80 B. 中位數是75 C. 平均數是80 D. 極差是15
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2008北京奧運會主會場“鳥巢”的座席數是91 000個,這個數用科學記數法表示為( )
A. 0.91×105 B. 9.1×104 C. 91×103 D. 9.1×103
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com