
【題目】如圖,把Rt△ABC放在平面直角坐標系內,其中∠CAB=90°,BC=13,點A、B的坐標分別為(1,0),(6,0),將△ABC沿x軸向右平移,當點C落在直線y=2x﹣4上時,線段BC掃過的面積為( )

A.84B.80C.91D.78
科目:初中數學 來源: 題型:
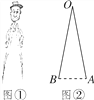
【題目】如圖①是一副創(chuàng)意卡通圓規(guī),圖②是其平面示意圖,OA是支撐臂,OB是旋轉臂.使用時,以點A為支撐點,鉛筆芯端點B可繞點A旋轉作出圓.已知OA=OB=10cm.
(1)當∠AOB=18°時,求所作圓的半徑(結果精確到0.01cm);
(2)保持∠AOB=18°不變,在旋轉臂OB末端的鉛筆芯折斷了一截的情況下,作出的圓與(1)中所作圓的大小相等,求鉛筆芯折斷部分的長度(結果精確到0.01cm,參考數據:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科學計算器).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了抓住文化藝術節(jié)的商機,某商店決定購進 A、B 兩種藝術節(jié)紀念品,若購進 A 種紀念品 8 件,B 種紀念品 3 件,需要 950 元;若購進A 種紀念品 5 件,B 種紀念品 6 件,需要 800 元.
(1)求購進A、B 兩種紀念品每件各需多少元?
(2)若該商店決定購進這兩種紀念品共 100 件,考慮市場需求和資金周轉,用于購買這 100 件紀念品的資金不少于 7000 元,但不超過 7500 元,那么該商店共有幾種進貨方案?
(3)若銷售每件 A 件紀念品可獲利潤 20 元,每件 B 種紀念品可獲利潤 30 元,在第(2)問的各種進貨方案中,哪一種方案獲利最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=56°,OC平分∠AOB,如果射線OA上的點E滿足△OCE是等腰三角形,那么∠OEC的度數為________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的頂點P是BC的中點,兩邊PE、PF分別交AB、AC于點E、F,當∠EPF在△ABC內繞點P旋轉時,下列結論①EF=AP;②△EPF為等腰直角三角形;③AE=CF;④S四邊形AEPF![]() ,正確的有( )
,正確的有( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,梯形ABCD中,AD∥BC,CD⊥BC,已知AB=5,BC=6,cosB=![]() .點O為BC邊上的動點,以O為圓心,BO為半徑的⊙O交邊AB于點P.
.點O為BC邊上的動點,以O為圓心,BO為半徑的⊙O交邊AB于點P.
(1)設OB=x,BP=y,求y與x的函數關系式,并寫出函數定義域;
(2)當⊙O與以點D為圓心,DC為半徑⊙D外切時,求⊙O的半徑;
(3)連接OD、AC,交于點E,當△CEO為等腰三角形時,求⊙O的半徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】西南大學附中一年一度的“繽紛節(jié)”受到社會各界的高度贊揚,2018年12月14日西南大學附中成功舉辦了第十八屆繽紛節(jié),為成功籌辦此次繽紛節(jié),學校后勤工作人員進行了繁瑣細致地準備工作,為了搭建舞臺、后勤服務平臺和安排全校師生及家長朋友們的座位,學校需要購買鋼材1380根,購買膠板凳2300個.現安排A,B兩種型號的貨車共10輛運往學校,已知一輛A型貨車可以用150根鋼材和200個板凳裝滿,一輛B型貨車可以用120根鋼材和350個板凳裝滿,并且一輛A型貨車的運費為500元,一輛B型貨車的運費為520元;設運輸鋼材和板凳的總費用為y元,租用A型貨車x輛.
(1)試寫出y與x之間的函數關系式,并寫出x的取值范圍;
(2)按要求有哪幾種運輸方案,運費最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國古代稱直角三角形為“勾股形”,并且直角邊中較短邊為勾,另一直角邊為股,斜邊為弦.如圖1所示,數學家劉徽(約公元225年—公元295年)將勾股形分割成一個正方形和兩對全等的直角三角形,后人借助這種分割方法所得的圖形證明了勾股定理.如圖2所示的長方形,是由兩個完全相同的“勾股形”拼接而成,若![]() ,
,![]() ,則長方形的面積為______.
,則長方形的面積為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖所示的正方形網格中,每個小正方形的邊長都是1, ![]() 的頂點都在正方形網格的格點(網格線的交點)上.
的頂點都在正方形網格的格點(網格線的交點)上.

(1)請在圖中的網格平面內畫出平面直角坐標系,使點![]() 坐標為(7,6),點
坐標為(7,6),點![]() 坐標為(2,1);
坐標為(2,1);
(2)在(1)的條件下,
①請畫出點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() ,并寫出點
,并寫出點![]() 的坐標;
的坐標;
②點![]() 是邊
是邊![]() 上的一個動點,連接
上的一個動點,連接![]() ,則
,則![]() 周長的最小值為 .
周長的最小值為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com