某市區一條主要街道的改造工程有甲、乙兩個工程隊投標．經測算：若由兩個工程隊合做，12天恰好完成；若兩個隊合做9天后，剩下的由甲隊單獨完成，還需5天時間，現需從這兩個工程隊中選出一個隊單獨完成，從縮短工期角度考慮，你認為應該選擇哪個隊？為什么？
科目：初中數學 來源： 題型：
某景區內的環形路是邊長為800米的正方形ABCD，如圖1和圖2．現有1號、2號兩游覽車分別從出口A和景點C同時出發，1號車順時針、2號車逆時針沿環形路連續循環行駛，供游客隨時免費乘車（上、下車的時間忽略不計），兩車速度均為200米/分．
探究：設行駛吋間為t分．
（1）當0≤t≤8時，分別寫出1號車、2號車在左半環線離出口A的路程y1，y2（米） 與t（分）的函數關系式，并求出當兩車相距的路程是400米時t的值；
（2）t為何值時，1號車第三次恰好經過景點C？并直接寫出這一段時間內它與2號車相遇過的次數．
發現：如圖2，游客甲在BC上的一點K（不與點B，C重合）處候車，準備乘車到出口A，設CK=x米．
情況一：若他剛好錯過2號車，便搭乘即將到來的1號車；
情況二：若他剛好錯過1號車，便搭乘即將到來的2號車．
比較哪種情況用時較多？（含候車時間）
決策：己知游客乙在DA上從D向出口A走去．步行的速度是50米/分．當行進到DA上一點P （不與點D，A重合）時，剛好與2號車迎面相遇．
（1）他發現，乘1號車會比乘2號車到出口A用時少，請你簡要說明理由：
（2）設PA=s（0＜s＜800）米．若他想盡快到達出口A，根據s的大小，在等候乘1號車還是步行這兩種方式中．他該如何選擇？
查看答案和解析>>
科目：初中數學 來源： 題型：
關于反比例函數y=
的圖象，下列說法正確的是（ ）
A．圖象經過點（1，1） B． 兩個分支分布在第二、四象限
C．兩個分支關于x軸成軸對稱 D． 當x＜0時，y隨x的增大而減小
查看答案和解析>>
科目：初中數學 來源： 題型：
平面直角坐標系中，四邊形ABCD是菱形，點C的坐標為（﹣3，4），點A在x軸的正半軸上，O為坐標原點，連接OB，拋物線y=ax2+bx+c經過C、O、A三點．
（1）直接寫出這條拋物線的解析式；
（2）如圖1，對于所求拋物線對稱軸上的一點E，設△EBO的面積為S1，菱形ABCD的面積為S2，當S1≤
S2時，求點E的縱坐標n的取值范圍；
（3）如圖2，D（0，﹣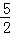
）為y軸上一點，連接AD，動點P從點O出發，以
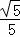個單位/秒的速度沿OB方向運動，1秒后，動點Q從O出發，以2個單位/秒的速度沿折線O﹣A﹣B方向運動，設點P運動時間為t秒（0＜t＜6），是否存在實數t，使得以P、Q、B為頂點的三角形與△ADO相似？若存在，求出相應的t值；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖7，正方形ABCD的對角線相交于點O，∠CAB的平分線分別交BD、BC于E、F，作BH⊥AF于點H，分別交AC、CD于點G、P，連結GE、GF．
（1）求證：△OAE ≌△OBG．
（2）試問：四邊形BFGE是否為菱形?若是，請證明；若不是，請說明理由．
（3）試求：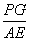
的值（結果保留根號）．
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
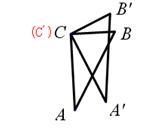
如圖，兩塊完全相同的含30°角的直角三角板ABC和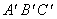
重合在一起，將三角板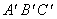繞其頂點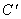
按逆時針方向旋轉角α（0°< α≤90°），有以下四個結論：
①當α=30°時，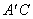
與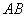
的交點恰好為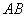的中點；②當α=60°時，
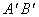恰好經過點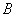
；
③在旋轉過程中，存在某一時刻，使得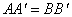
； ④在旋轉過程中，始終存在
，其中結論正確的序號是 .(多填或填錯得0分，少填酌情給分）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
×9+
×5=1，
=
，
）﹣2+
﹣2sin45°﹣|1﹣
|．
