
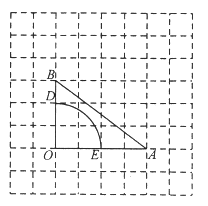
【題目】如圖,在每個(gè)小正方形的邊長為![]() 的網(wǎng)格中,
的網(wǎng)格中,![]() 的頂點(diǎn)
的頂點(diǎn)![]() 均在格點(diǎn)上,點(diǎn)
均在格點(diǎn)上,點(diǎn)![]() 在
在![]() 上,且點(diǎn)
上,且點(diǎn)![]() 也在格點(diǎn)上.
也在格點(diǎn)上.
(Ⅰ)![]() 的值為_____________;
的值為_____________;
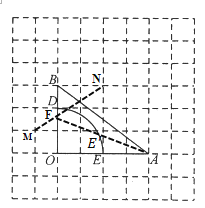
(Ⅱ)![]() 是以點(diǎn)
是以點(diǎn)![]() 為圓心,
為圓心,![]() 為半徑的一段圓弧.在如圖所示的網(wǎng)格中,將線段
為半徑的一段圓弧.在如圖所示的網(wǎng)格中,將線段![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)得到
逆時(shí)針旋轉(zhuǎn)得到![]() ,旋轉(zhuǎn)角為,連接
,旋轉(zhuǎn)角為,連接![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 的值最小時(shí),請用無刻度的直尺畫出點(diǎn)
的值最小時(shí),請用無刻度的直尺畫出點(diǎn)![]() ,并簡要說明點(diǎn)
,并簡要說明點(diǎn)![]() 的位置是如何找到的(不要求證明)______.
的位置是如何找到的(不要求證明)______.
【答案】(Ⅰ)![]() (Ⅱ)取格點(diǎn)
(Ⅱ)取格點(diǎn)![]() ,連接
,連接![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ;連接
;連接![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 即為所求.
即為所求.
【解析】
(Ⅰ)根據(jù)網(wǎng)格中OB和OE的長直接得出比值即可
(Ⅱ)取格點(diǎn)![]() ,連接
,連接![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ;連接
;連接![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 即為所求.
即為所求.
解:(Ⅰ)∵由圖可得OB=3,OE=2
∴![]() ;
;
故答案為:![]()
(Ⅱ)取格點(diǎn)![]() ,連接
,連接![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ;連接
;連接![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 即為所求.
即為所求.
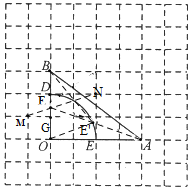
說明:線段![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)得到
逆時(shí)針旋轉(zhuǎn)得到![]() ,則
,則![]() ,
,
連接![]() 并延長交OB于點(diǎn)F,則
并延長交OB于點(diǎn)F,則![]() 的值最小,要使
的值最小,要使![]() 的值最小,需讓
的值最小,需讓![]() ,即
,即![]() ,連接
,連接![]() ,
,![]() ,此時(shí)若△FOE′∽△E′OB,可得
,此時(shí)若△FOE′∽△E′OB,可得![]() ,
,
則只需OF=![]() ,需GF=
,需GF=![]() ,只需將線段DG分為2:1即可,∴取DN=2,GM=1MN 交OB于點(diǎn)F連接AF交
,只需將線段DG分為2:1即可,∴取DN=2,GM=1MN 交OB于點(diǎn)F連接AF交![]() 于點(diǎn)
于點(diǎn)![]() ..
..


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AD∥BC,CE平分∠BCD,∠DAC=3∠BCD,∠ACD=20°,當(dāng)AB與AC互相垂直時(shí),∠B的度數(shù)為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長為4的正方形![]() 中,
中,![]() 是
是![]() 邊上的兩個(gè)動(dòng)點(diǎn),且
邊上的兩個(gè)動(dòng)點(diǎn),且![]() ,連接
,連接![]() ,
,![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,連接
,連接![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() ,下列結(jié)論:①
,下列結(jié)論:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() ;⑤線段
;⑤線段![]() 的最小值是
的最小值是![]() .正確的個(gè)數(shù)有( )
.正確的個(gè)數(shù)有( )
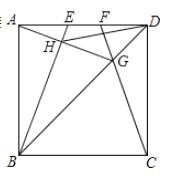
A.2個(gè)B.3個(gè)C.4個(gè)D.5個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,某公園內(nèi)有一座古塔AB,在塔的北面有一棟建筑物,某日上午9時(shí)太陽光線與水平面的夾角為32°,此時(shí)塔在建筑物的墻上留下了高3米的影子CD.中午12時(shí)太陽光線與地面的夾角為45°,此時(shí)塔尖A在地面上的影子E與墻角C的距離為15米(B、E、C在一條直線上),求塔AB的高度.(結(jié)果精確到0.01米)
參考數(shù)據(jù):sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249,![]() .
.
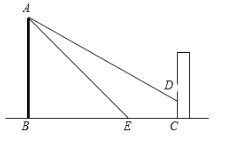
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為弘揚(yáng)傳統(tǒng)文化,某校開展了“傳承經(jīng)典文化,閱讀經(jīng)典名著”活動(dòng).為了解七、八年級(jí)學(xué)生(七、八年級(jí)各有600名學(xué)生)的閱讀效果,該校舉行了經(jīng)典文化知識(shí)競賽.現(xiàn)從兩個(gè)年級(jí)各隨機(jī)抽取20名學(xué)生的競賽成績(百分制)進(jìn)行分析,過程如下:
收集數(shù)據(jù):
七年級(jí):79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年級(jí):92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理數(shù)據(jù):
|
|
|
|
|
| |
七年級(jí) | 0 | 1 | 0 | a | 7 | 1 |
八年級(jí) | 1 | 0 | 0 | 7 | b | 2 |
分析數(shù)據(jù):
平均數(shù) | 眾數(shù) | 中位數(shù) | |
七年級(jí) | 78 | 75 |
|
八年級(jí) | 78 |
| 80.5 |
應(yīng)用數(shù)據(jù):
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估計(jì)該校七、八兩個(gè)年級(jí)學(xué)生在本次競賽中成績在90分以上的共有多少人?
(3)你認(rèn)為哪個(gè)年級(jí)的學(xué)生對經(jīng)典文化知識(shí)掌握的總體水平較好,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() (
(![]() ,
,![]() 是常數(shù),且
是常數(shù),且![]() ),經(jīng)過點(diǎn)
),經(jīng)過點(diǎn)![]() ,
,![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
(Ⅰ)求拋物線的解析式;
(Ⅱ)若點(diǎn)![]() 是射線
是射線![]() 上一點(diǎn),過點(diǎn)
上一點(diǎn),過點(diǎn)![]() 作
作![]() 軸的垂線,垂足為點(diǎn)
軸的垂線,垂足為點(diǎn)![]() ,交拋物線于點(diǎn)
,交拋物線于點(diǎn)![]() ,設(shè)
,設(shè)![]() 點(diǎn)橫坐標(biāo)為
點(diǎn)橫坐標(biāo)為![]() ,線段
,線段![]() 的長為
的長為![]() ,求出
,求出![]() 與
與![]() 之間的函數(shù)關(guān)系式,并寫出相應(yīng)的自變量
之間的函數(shù)關(guān)系式,并寫出相應(yīng)的自變量![]() 的取值范圍;
的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,當(dāng)點(diǎn)![]() 在線段
在線段![]() 上時(shí),設(shè)
上時(shí),設(shè)![]() ,已知
,已知![]() ,
,![]() 是以
是以![]() 為未知數(shù)的一元二次方程
為未知數(shù)的一元二次方程![]() (
(![]() 為常數(shù))的兩個(gè)實(shí)數(shù)根,點(diǎn)
為常數(shù))的兩個(gè)實(shí)數(shù)根,點(diǎn)![]() 在拋物線上,連接
在拋物線上,連接![]() ,
,![]() ,
,![]() ,且
,且![]() 平分
平分![]() ,求出
,求出![]() 值及點(diǎn)
值及點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,直線l:y=kx+b(k≠0)與反比例函數(shù)y![]() 的圖象的一個(gè)交點(diǎn)為M(1,m).
的圖象的一個(gè)交點(diǎn)為M(1,m).
(1)求m的值;
(2)直線l與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,連接OM,設(shè)△AOB的面積為S1,△MOB的面積為S2,若S1≥3S2,求k的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 為
為![]() 的直徑,
的直徑,![]() 為
為![]() 上一點(diǎn),連接
上一點(diǎn),連接![]() ,過
,過![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() ,其中
,其中![]() 交
交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() .
.
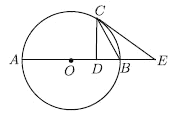
(1)求證:![]() 是
是![]() 的切線.
的切線.
(2)如圖,點(diǎn)![]() 在
在![]() 上,且滿足
上,且滿足![]() ,連接
,連接![]() 并延長交
并延長交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() .
.
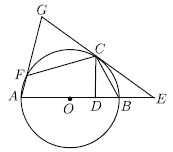
①試探究線段![]() 與
與![]() 之間滿足的數(shù)量關(guān)系.
之間滿足的數(shù)量關(guān)系.
②若![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
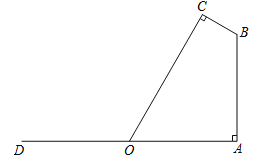
【題目】如圖,若要在寬AD為20米的城南大道兩邊安裝路燈,路燈的燈臂BC長2米,且與燈柱AB成120°角,路燈采用圓錐形燈罩,燈罩的軸線CO與燈臂BC垂直,當(dāng)燈罩的軸線CO通過公路路面的中心線時(shí)照明效果最好,此時(shí),路燈的燈柱AB高應(yīng)該設(shè)計(jì)為多少米(結(jié)果保留根號(hào))?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com