科目：初中數學 來源： 題型：
已知拋物線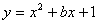
的頂點在x軸上，且與y軸交于A點. 直線
經過A、B兩點，點B的坐標為（3，4）.
（1）求拋物線的解析式，并判斷點B是否在拋物線上；
（2）如果點B在拋物線上，P為線段AB上的一個動點（點P與A、B不重合），過P作x軸的垂線與這個二次函數的圖象交于點E，設線段PE的長為h ，點P的橫坐標為x.當x為何值時，h取得最大值，求出這時的h值.
查看答案和解析>>
科目：初中數學 來源： 題型：
閱讀下面材料：
定義：與圓的所有切線和割線都有公共點的幾何圖形叫做這個圓的關聯圖形．
問題：⊙O的半徑為1，畫一個⊙O的關聯圖形．
 |
個問題時，小明以O為原點建立平面直角坐標系xOy進行探究，他發現能畫出很多⊙O的關聯圖形，例如：⊙O本身和圖1中的△ABC（它們都是封閉的圖形），以及圖2中以O為圓心的 （它是非封閉的圖形），它們都是⊙O的
關聯圖形．而圖2中以P，Q為端點的一條曲線就不是⊙O的關聯圖形． 參考小明的發現，解決問題：
（1）在下列幾何圖形中，⊙O的關聯圖形是 （填序號）；
① ⊙O的外切正多邊形
② ⊙O的內接正多邊形
③ ⊙O的一個半徑大于1的同心圓
（2）若圖形G是⊙O的關聯圖形，并且它是封閉的，則圖形G的周長的最小值是____；
（3）在圖2中，當⊙O的關聯圖形 的弧長最小時，經過D，E兩點的直線為y =__；
（4）請你在備用圖中畫出一個⊙O的關聯圖形，所畫圖形的長度l小于（2）中圖形G的周長的最小值，并寫出l的值（直接畫出圖形，不寫作法）．
查看答案和解析>>
科目：初中數學 來源： 題型：
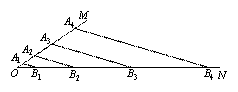
如圖，點A1、A2 、A3 、…，點B1、B2 、B3 、…，分別在射線OM、ON上，A1B1∥A2B2∥A3B3∥A4B4∥…．如果A1B1=2，A1A2=2OA1，A2A3=3OA1，A3A 4=4OA1，…．
那么A2B2= ，AnBn= ．（n為正整數）
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
操作與探究
我們知道：過任意一個三角形的三個頂點能作一個圓，探究過四邊形四個頂點作圓的條件。
（1）分別測量下面各四邊形的內角，如果過某個四邊形的四個頂點能一個圓，那么其相對的兩個角之間有什么關系？證明你的發現.
(2) 如果過某個四邊形的四個頂點不能一個圓，那么其相對的兩個角之間有上面的關系嗎？試結合下面的兩個圖說明其中的道理.（提示：考慮
）
由上面的探究，試歸納出判定過四邊形的四個頂點能作一個圓的條件.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
中，
、
分別是
、
邊上的點，且
，如果
,那么
的值為( ) 
B. 
C. 
D. 
是⊙
的切線， 
為切點，
的延長線交⊙
點，連接
，若
，
，則
等于( ) A. 4 B.6 C. 
D. 
．若AB＝6，DC＝4，PD＝2，求PB的長．
的半徑為5，
，垂足為
，那么
的長是（ ）
先沿
軸向右平移1個單位， 再沿
軸向上移2個單位，所得拋物線的解析式是
B．
D．