Question

2．請從以下A、B兩題中任選一題解答，若兩題都做，按A題給分．
A．如圖1，△ABC和△FED均為等腰直角三角形，AC與BE重合，AB=AC=EF=3，∠BAC=∠DEF=90°，固定△ABC，將△DEF繞點A順時針旋轉，當DF邊與AB重合時，旋轉停止．現不考慮旋轉開始和結束時重合的情況，設DE、DF（或它們的延長線）分別交BC（或它的延長線）于G、H點，如圖2．
（1）始終與△AGC相似的三角形是△HAB和△HGA；
（2）設CG=x，BH=y，求y關于x的函數關系式（只要求根據圖2的情形說明理由）；
（3）在整個旋轉過程中，當旋轉角為多少度時，△AGH是等腰三角形？請直接寫出旋轉的度數．
B．如圖（1），正方形AEFG的邊長為1，正方形ABCD的邊長為3，且點F在AD上；
（1）求S_△DBF；
（2）把正方形AEFG繞點A按逆時針方向旋轉45°得到圖（2）中的S_△DBF；
（3）將正方形AEFG繞點A旋轉一周，在旋轉的過程中，S_△DBF存在最大值與最小值，請直接寫出最大值為$\frac{15}{2}$，最小值為$\frac{3}{2}$．
我選做的是A題．

Answer 1

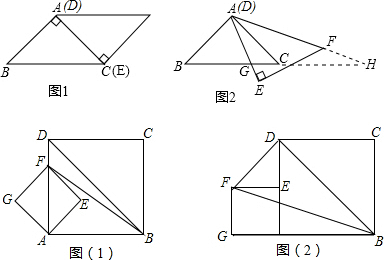
分析 A（1）根據等腰直角三角形和旋轉的性質得出：∠B=∠ACB=∠HAG=45°，∠CAG=∠H，即可判斷；
（2）由（1）運用：△AGC∽△HAB得出線段比相等，代入常量和變量即可；
（3）分類討論等腰三角形，求出旋轉角：∠CAG即可．
B（1）運用正方形性質求出DF和AB，再根據三角形面積公式求解即可；
（2）連接AF，證明AF∥BD，根據三角形ABD的面積求解；
（3）以點A為圓心以AF長為半徑畫圓，交過點A與BD垂直的直線于點F″，F′，
由題意可知BD的長為定值，當F轉至F″時三角形面積最大，轉至點F′時三角形面積最小，根據三角形面積公式求值．

解答 解：A．
（1）由等腰直角三角形的性質和旋轉的性質可知：∠B=∠ACB=∠HAG=45°，∠CAG=∠H，
∴始終與△AGC相似的三角形是：△HAB和△HGA；
（2）由（1）知：△AGC∽△HAB，
∴$\frac{CG}{AB}=\frac{AC}{BH}$，即$\frac{x}{3}=\frac{3}{y}$，
∴y=$\frac{9}{x}$；
（3）如圖：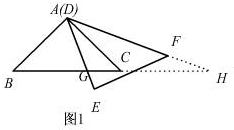

由題意可知：∠HAG=45°，且在旋轉過程中保持不變，
當AG=HG時，∠H=∠HAG=45°，可求∠AGH=90°，
∴∠GAC=90°-45°=45°，
此時，旋轉角為45°；
當AG=AH時，∠AGH=（180°-45°）÷2=62.5°，
∴∠GAC=180°-45°-62.5°=62.5°，
此時，旋轉角為62.5°；
當AH=GH時，∠AGH=∠HAG=45°，（E與B重合，舍去）
綜上所述：當旋轉角為62.5°或45°時，△AGH是等腰三角形．
B．（1）如圖1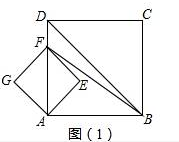

由正方形AEFG的邊長為1，正方形ABCD的邊長為3，可求AF=$\sqrt{A{E}^{2}+E{F}^{2}}$=$\sqrt{2}$，AD=AB=3，
DF=AD-AF=3-$\sqrt{2}$，
∴S_△DBF=$\frac{1}{2}$DF×AB=$\frac{9}{2}$-$\frac{3}{2}\sqrt{2}$，
（2）如圖2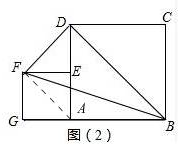

連接AF，可知∠FAG=∠DBA=45°，
∴AF∥BD，
∴S_△DBF=S_△ABD=$\frac{1}{2}$×AB×AD=$\frac{1}{2}$×3×3=$\frac{9}{2}$；
（3）如圖3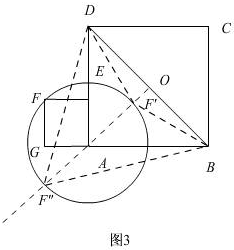

以點A為圓心以AF長為半徑畫圓，交過點A與BD垂直的直線于點F″，F′，
由題意可知BD的長為定值，當F轉至F″時三角形面積最大，轉至點F′時三角形面積最小，
在正方形ABCD中，可求OA=$\frac{3}{2}\sqrt{2}$，
∴OF″=$\sqrt{2}$+$\frac{3}{2}\sqrt{2}$，OF′=$\frac{3}{2}\sqrt{2}$-$\sqrt{2}$，
S_△DBF的最大面積=$\frac{1}{2}×3\sqrt{2}$×（$\sqrt{2}$$+\frac{3}{2}\sqrt{2}$）=$\frac{15}{2}$，
S_△DBF的最小面積=$\frac{1}{2}×3\sqrt{2}$×（$\frac{3}{2}\sqrt{2}$-$\sqrt{2}$）=$\frac{3}{2}$．

點評 此題主要考查圖形的旋轉變換問題，知道旋轉的相關性質，會分類討論等腰三角形是解題的關鍵．