
【題目】(問題提出)
如圖①,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 邊上的中線
邊上的中線![]() 的取值范圍.
的取值范圍.
(1)(問題解決)
解決此問題可以用如下方法:延長![]() 到點
到點![]() 使
使![]() ,再連接
,再連接![]() (或將
(或將![]() 繞著點
繞著點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ),把
),把![]() 、
、![]() 、
、![]() 集中在
集中在![]() 中,利用三角形三邊的關系即可判斷,由此得出中線
中,利用三角形三邊的關系即可判斷,由此得出中線![]() 的取值范圍.
的取值范圍.
(2)(應用)
如圖②,在![]() 中,
中,![]() 為
為![]() 的中點,已知
的中點,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的長.
的長.
(3)(拓展)
如圖③,在![]() 中,
中,![]() ,點
,點![]() 是邊
是邊![]() 的中點,點
的中點,點![]() 在邊
在邊![]() 上,過點
上,過點![]() 作
作![]() 交邊
交邊![]() 于點
于點![]() ,連接
,連接![]() 。已知
。已知![]() ,
,![]() ,求
,求![]() 的長.
的長.

【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() .
.
【解析】
(1)延長AD到E,使AD=DE,連接BE,證△ADC≌△EDB,推出EB=AC,根據三角形的三邊關系求出即可;
(2)同(1)可證△ADC≌△EDB,可得△ABE的三邊長,利用勾股定理的逆定理得出△ABE為直角三角形,然后在Rt△BED中利用勾股定理求出BD的長,進而得出BC的長;
(3)延長ED到點G,使DG=ED,連接CG,FG.由△EBD≌△GCD可得∠B=∠GCD、BE=CG=4,根據∠A=90°知∠GCF=90°,利用勾股定理求得FG的長,最后由中垂線性質即可得EF=FG.
(1)解:延長AD到E,使AD=DE,連接BE,
∵AD是△ABC的中線,
∴BD=CD,
在△ADC與△EDB中,
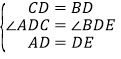 ,
,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根據三角形的三邊關系得:AB-AC<AE<AC+AB,
∴2<AE<10,
∵AE=2AD,
∴,1<AD<5,
即:BC邊上的中線AD的取值范圍1<AD<5;
(2)
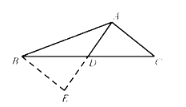
延長AD至E,使DE=AD,連接BE.
∵點D為邊BC的中點,
∴BD=CD.
∵∠BDE=∠ADC,
∴△ADC≌△EDB.
∴BE=AC=3,DE=AD=2.
∴AE=4.
∵AB=5,且![]() ,
,
∴![]() .
.
∴△ABE為直角三角形,∠AEB=90°.
∵在Rt△BDE中,∠BED=90°,
∴BD=![]() ,
,
∴BC=2BD=![]() ;
;
(3)

延長ED到點G,使DG=ED,連接CG,FG.
同前法可得△EBD≌△GCD,
∴∠B=∠GCD,BE=CG=4,
又∵∠A=90°,
∴∠B+∠BCA=90°,
∴∠GCD+∠BCA=90°,即∠GCF=90°,
∵CG=4,CF=5,
∴FG=![]() =
=![]() =
=![]() .
.
∴EF= FG =![]() .
.


科目:初中數學 來源: 題型:
【題目】在同一副撲克牌中取出6張撲克牌,分別是黑桃2、4、6,紅心6、7、8.將撲克牌背面朝上分別放在甲、乙兩張桌面上,先從甲桌面上任意摸出一張黑桃,再從乙桌面上任意摸出一張紅心.
(1)表示出所有可能出現的結果;
(2)小黃和小石做游戲,制定了兩個游戲規則:
規則1:若兩次摸出的撲克牌中,至少有一張是“6”,小黃贏;否則,小石贏.
規則2:若摸出的紅心牌點數是黑桃牌點數的整數倍時,小黃贏;否則,小石贏.
小黃想要在游戲中獲勝,會選擇哪一條規則,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知正方形ABCO,A(0,3),點D為x軸上一動點,以AD為邊在AD的右側作等腰Rt△ADE,∠ADE=90°,連接OE,則OE的最小值為________.
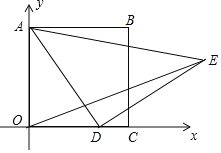
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線經過點A(﹣1,0),B(4,0),C(0,2)三點,點D與點C關于x軸對稱,點P是x軸上的一個動點,設點P的坐標為(m,0),過點P做x軸的垂線l交拋物線于點Q,交直線BD于點M.
(1)求該拋物線所表示的二次函數的表達式;
(2)已知點F(0,![]() ),當點P在x軸上運動時,試求m為何值時,四邊形DMQF是平行四邊形?
),當點P在x軸上運動時,試求m為何值時,四邊形DMQF是平行四邊形?
(3)點P在線段AB運動過程中,是否存在點Q,使得以點B、Q、M為頂點的三角形與△BOD相似?若存在,求出點Q的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
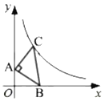
【題目】如圖,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 是
是![]() 軸正半軸上一點,以
軸正半軸上一點,以![]() 為邊作等腰直角三角形
為邊作等腰直角三角形![]() ,使
,使![]() ,點
,點![]() 在第一象限。若點
在第一象限。若點![]() 在函數
在函數![]() 的圖象上,則
的圖象上,則![]() 的面積為( )
的面積為( )
A. ![]() .B.
.B. ![]() .C.
.C. ![]() .D.
.D. ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
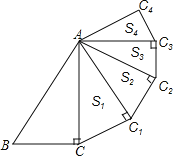
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 為斜邊作
為斜邊作![]() ,使
,使![]() ,
,![]() 的面積記為
的面積記為![]() ,則
,則![]() ______;再以
______;再以![]() 為斜邊作
為斜邊作![]() ,使
,使![]() ,
,![]() 的面積記為
的面積記為![]() ,……,以此類推,則
,……,以此類推,則![]() ______.(用含
______.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
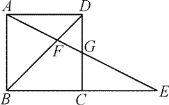
【題目】如圖,在正方形ABCD中,G為CD邊中點,連接AG并延長,分別交對角線BD于點F,交BC邊延長線于點E.若FG=2,則AE的長度為( )
A. 6B. 8
C. 10D. 12
查看答案和解析>>
科目:初中數學 來源: 題型:
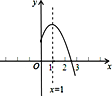
【題目】如圖是二次函數![]() (a,b,c是常數,a≠0)圖象的一部分,與x軸的交點A在點(2 ,0)和(3 ,0)之間,對稱軸是x=1.對于下列結論:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m為實數);⑤ 當-1<x<3時,y>0. 其中正確結論的個數為( )
(a,b,c是常數,a≠0)圖象的一部分,與x軸的交點A在點(2 ,0)和(3 ,0)之間,對稱軸是x=1.對于下列結論:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m為實數);⑤ 當-1<x<3時,y>0. 其中正確結論的個數為( )
A. 2個B. 3個C. 4個D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
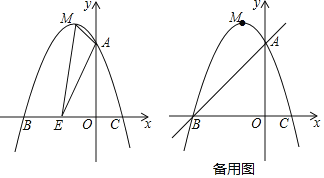
【題目】如圖,拋物線y=ax2+bx+3交y軸于點A,交x軸于點B(-3,0)和點C(1,0),頂點為點M.
(1)求拋物線的解析式;
(2)如圖,點E為x軸上一動點,若△AME的周長最小,請求出點E的坐標;
(3)點F為直線AB上一個動點,點P為拋物線上一個動點,若△BFP為等腰直角三角形,請直接寫出點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com