
【題目】如圖1,已知線段AB=16cm,點C為線段AB上的一個動點,點D、E分別是AC和BC的中點.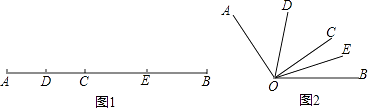
(1)若點C恰為AB的中點,求DE的長;
(2)若AC=6cm,求DE的長;
(3)試說明不論AC取何值(不超過16cm),DE的長不變;
(4)知識遷移:如圖2,已知∠AOB=130°,過角的內部任一點C畫射線OC,若OD、OE分別平分∠AOC和∠BOC,試說明∠DOE=65°與射線OC的位置無關.
【答案】
(1)解:∵點C恰為AB的中點,
∴AC=BC= ![]() AB=8cm,
AB=8cm,
∵點D、E分別是AC和BC的中點,
∴DC= ![]() AC=4cm,CE=
AC=4cm,CE= ![]() BC=4cm,
BC=4cm,
∴DE=8cm
(2)解:∵AB=16cm,AC=6cm,
∴BC=10cm,
由(1)得,DC= ![]() AC=3cm,CE=
AC=3cm,CE= ![]() CB=5cm,
CB=5cm,
∴DE=8cm
(3)解:∵點D、E分別是AC和BC的中點,
∴DC= ![]() AC,CE=
AC,CE= ![]() BC,
BC,
∴DE= ![]() (AC+BC)=
(AC+BC)= ![]() AB,
AB,
∴不論AC取何值(不超過16cm),DE的長不變
(4)解:∵OD、OE分別平分∠AOC和∠BOC,
∴∠DOC= ![]() ∠AOC,∠EOC=
∠AOC,∠EOC= ![]() ∠BOC,
∠BOC,
∴∠DOE=∠DOC+∠EOC= ![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ![]() ∠AOB=65°,
∠AOB=65°,
∴∠DOE=65°與射線OC的位置無關
【解析】(1)由點C恰為AB的中點,得到AC=BC的值,再由點D、E分別是AC和BC的中點,求出DE的值;(2)由(1)得,DC=![]() AC的值,CE=
AC的值,CE=![]() CB的值,得到DE的值;(3)由點D、E分別是AC和BC的中點,得到不論AC取何值(不超過16cm),DE的長不變;(4)由OD、OE分別平分∠AOC和∠BOC,根據角平分線定義,得到∠DOE=∠DOC+∠EOC=
CB的值,得到DE的值;(3)由點D、E分別是AC和BC的中點,得到不論AC取何值(不超過16cm),DE的長不變;(4)由OD、OE分別平分∠AOC和∠BOC,根據角平分線定義,得到∠DOE=∠DOC+∠EOC=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB,得到∠DOE=65°與射線OC的位置無關.
∠AOB,得到∠DOE=65°與射線OC的位置無關.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】為了創設全新的校園文化氛圍,進一步組織學生開展課外閱讀,讓學生在豐富多彩的書海中,擴大知識源,親近母語,提高文學素養.某校準備開展“與經典為友、與名著為伴”的閱讀活動,活動前對本校學生進行了“你最喜歡的圖書類型(只寫一項)”的隨機抽樣調查,相關數據統計如下:
請根據以上信息解答下列問題: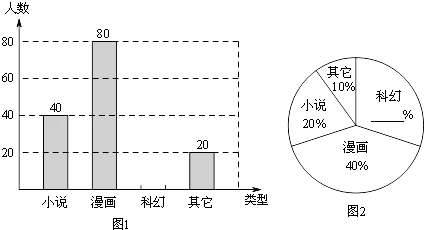
(1)該校對多少名學生進行了抽樣調查?
(2)請將圖1和圖2補充完整;并求出扇形統計圖中小說所對應的圓心角度數.
(3)已知該校共有學生800人,利用樣本數據估計全校學生中最喜歡小說人數約為多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市對進貨價為10元/千克的某種蘋果的銷售情況進行統計,發現每天銷售量y(千克)與銷售價x(元/千克)存在一次函數關系,如圖所示.
(1)求y關于x的函數關系式(不要求寫出x的取值范圍);
(2)應怎樣確定銷售價,使該品種蘋果的每天銷售利潤最大?最大利潤是多少?
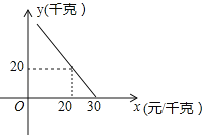
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據報道,某小區居民李先生改進用水設備,在十年內幫助他居住小區的居民累計節水300 000噸.將300 000用科學記數法表示應為( )
A.0.3×106
B.3×105
C.3×106
D.30×104
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,對角線AC、BD相交于點O,下列條件不能判定這個四邊形是平行四邊形的是( ) 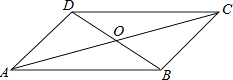
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB∥DC,AD=BC
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com