Question

在Rt△ABC中，∠C=90°，AC=3，BC=4，CP、CM分別是AB上的高和中線，如果圓A是以點A為圓心，半徑長為2的圓，那么下列判斷正確的是（ ）
A．點P，M均在圓A內
B．點P、M均在圓A外
C．點P在圓A內，點M在圓A外
D．點P在圓A外，點M在圓A內

Answer 1

【答案】分析：先利用勾股定理求得AB的長，再根據面積公式求出CP的長，根據勾股定理求出AP的長，根據中線的定義求出AM的長，然后由點P、M到A點的距離判斷點P、M與圓A的位置關系即可．
解答：解：∵在Rt△ABC中，∠C=90°，AC=3，BC=4，
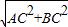
∴AB==5，
∵CP、CM分別是AB上的高和中線，
∴AB•CP=AC•BC，AM=AB=2.5，
∴CP=，
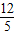
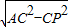
∴AP==1.8，
∵AP=1.8＜2，AM=2.5＞2，
∴點P在圓A內、點M在圓A外
故選C．
點評：本題考查了點與圓的位置關系的判定，根據點與圓心之間的距離和圓的半徑的大小關系作出判斷即可．