
【題目】近一周,各個學校均在緊張有序地進行中考模擬考試,學生們通過模擬考試來調整自己的狀態并了解自己的學業水平.某中學物理教研組想通過此次中考模擬的成績來預估中考的各個分數段人數,在全年級隨機抽取了男.女各40名學生的成績(滿分為80分,女生成績中最低分為45分),并將數據進行整理分析,給出了下面部分信息:
①男生成績扇形統計圖和女生成績頻數分布直方圖如下:(數據分組為A組:x<50;B組:50≤x<60;C組:60≤x<70;D組:70≤x≤80)

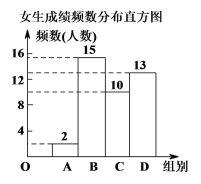
②男生C組中全部15名學生的成績為:
63,69,64,62,68,69,65,69,65,66,67,61,67,66,69.
③兩組數據的平均數.中位數.眾數.滿分率.極差(單位:分)如下表所示:
平均數 | 中位數 | 眾數 | 滿分率 | 極差 | |
男生 | 70 | b | c | 25% | 32 |
女生 | 70 | 68 | 78 | 15% | d |
(1)扇形統計圖A組學生中所對應的圓心角α的度數為 ,中位數b= ,眾數c= ,極差d= .
(2)通過以上的數據分析,你認為 (填“男生”或“女生”)的物理成績更好,并說明理由:
① ;② .
(3)若成績在70分(包含70分)以上為優秀,請你估計該校1200名學生中此次考試中優秀的人數.
【答案】(1)![]() ,
,![]() ,80,35;(2)男生,理由:①男生中位數
,80,35;(2)男生,理由:①男生中位數![]() 大于女生中位數68,整體情況較好;②男生極差32小于女生極差35,波動較小;(3)435人.
大于女生中位數68,整體情況較好;②男生極差32小于女生極差35,波動較小;(3)435人.
【解析】
(1)先求出B組和D組的人數,從而可得A組的人數,再根據A組人數的占比即可求出其所對應的圓心角的度數;根據中位數、眾數、極差的定義分別計算即可得;
(2)從中位數和極差的意義出發進行分析即可得;
(3)先出這40名男生和40名女生中,成績在70分(包含70分)以上的占比,再乘以1200即可得出答案.
(1)男生:B組有![]() (人),C組有15人,D組有
(人),C組有15人,D組有![]() (人)
(人)
則A組的人數為![]() (人)
(人)
因此,![]()
將男生C組學生的成績從小到大排列為:61,62,63,64,65,65,66,66,67,67,68,69,69,69,69
則男生40人中從小到大排列第20個是68,第21個是69
由中位數的定義得:![]() (分)
(分)
男生得滿分的有![]() (人)
(人)
由眾數的定義得:![]() (分)
(分)
女生最高分為80分,最低分為45分
則極差![]() (分)
(分)
故答案為:![]() ,
,![]() ,80,35;
,80,35;
(2)男生,理由如下:
①男生中位數![]() 大于女生中位數68,整體情況較好
大于女生中位數68,整體情況較好
②男生極差32小于女生極差35,波動較小
綜上,男生的物理成績更好;
(3)成績在70分(包含70分)以上的為優秀,即成績為D組學生為優秀
這40名男生和40名女生中,成績為D組的學生人數占比為![]()
則![]() (人)
(人)
答:該校1200名學生中,此次考試中優秀的人數為435人.


科目:初中數學 來源: 題型:
【題目】將一個正方形紙片AOBC放置在平面直角坐標系中,點A(0,4),點O(0,0),B(4,0),C(4,4)點.動點E在邊AO上,點F在邊BC上,沿EF折疊該紙片,使點O的對應點M始終落在邊AC上(點M不與A,C重合),點B落在點N處,MN與BC交于點P.
(Ⅰ)如圖①,當∠AEM=30°時,求點E的坐標;
(Ⅱ)如圖②,當點M落在AC的中點時,求點E的坐標;
(Ⅲ)隨著點M在AC邊上位置的變化,△MPC的周長是否發生變化?如變化,簡述理由;如不變,直接寫出其值.
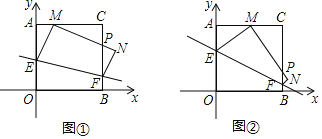
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為迎接2022年冬奧會,鼓勵更多的學生參與到志愿服務中來,甲、乙兩所學校組織了志愿服務團隊選拔活動,經過初選,兩所學校各有400名學生進入綜合素質展示環節.為了了解兩所學校這些學生的整體情況,從兩校進人綜合素質展示環節的學生中分別隨機抽取了50名學生的綜合素質展示成績(百分制),并對數據(成績)進行整理、描述和分析.下面給出了部分信息.
a.甲學校學生成績的頻數分布直方圖如下(數據分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
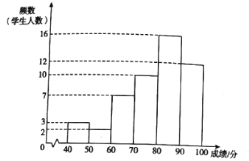
b.甲學校學生成績在![]() 這一組的是:
這一組的是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙學校學生成績的平均數、中位數、眾數、優秀率(85分及以上為優秀)如下:
平均數 | 中位數 | 眾數 | 優秀率 |
83.3 | 84 | 78 | 46% |
根據以上信息,回答下列問題:
(1)甲學校學生A,乙學校學生B的綜合素質展示成績同為83分,這兩人在本校學生中的綜合素質展示排名更靠前的是______(填“A”或“B”);
(2)根據上述信息,推斷_____學校綜合素質展示的水平更高,理由為_____(至少從兩個不同的角度說明推斷的合理性);
(3)若每所學校綜合素質展示的前120名學生將被選入志愿服務團隊,預估甲學校分數至少達到____分的學生才可以入選.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有甲,乙兩種機器人都被用來搬運某體育館室內裝潢材料甲型機器人比乙型機器人每小時少搬運30千克,甲型機器人搬運600千克所用的時間與乙型機器人搬運800千克所用的時間相同,兩種機器人每小時分別搬運多少千克?設甲型機器人每小時搬運x千克,根據題意,可列方程為( )
A. ![]() =
=![]() B.
B. ![]() =
=![]()
C. ![]() =
=![]() D.
D. ![]() =
=![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
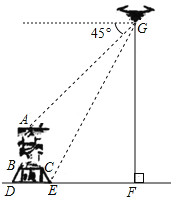
【題目】為了測量重慶有名的觀景點南山大金鷹的大致高度,小南同學使用的無人機進行觀察,當無人機與大金鷹側面在同一平面,且距離水平面垂直高度GF為100米時,小南調整攝像頭方向,當俯角為45°時,恰好可以拍攝到金鷹的頭頂A點;當俯角為63°時,恰好可以拍攝到金鷹底座點E.已知大金鷹是雄踞在一人造石臺上,石臺側面CE長12.5米,坡度為1:0.75,石臺上方BC長10米,頭部A點位于BC中點正上方.則金鷹自身高度約( )米.(結果保留一位小數,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=-![]() x2+
x2+![]() x+3與x軸交于A,B兩點(點A在點B左側),與y軸交于點C:連接BC,點P為線段BC上方拋物線上的一動點,連接OP交BC于點Q.
x+3與x軸交于A,B兩點(點A在點B左側),與y軸交于點C:連接BC,點P為線段BC上方拋物線上的一動點,連接OP交BC于點Q.
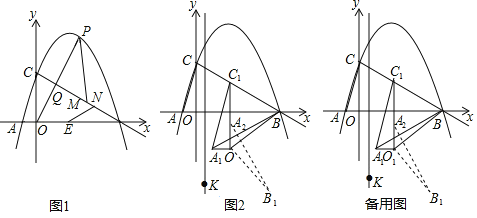
(1)如圖1,當![]() 值最大時,點E為線段AB上一點,在線段BC上有兩動點M,N(M在N上方),且MN=1,求PM+MN+NE-
值最大時,點E為線段AB上一點,在線段BC上有兩動點M,N(M在N上方),且MN=1,求PM+MN+NE-![]() BE的最小值;
BE的最小值;
(2)如圖2,連接AC,將△AOC沿射線CB方向平移,點A,C,O平移后的對應點分別記作A1,C1,O1,當C1B=O1B時,連接A1B、O1B,將△A1O1B繞點O1沿順時針方向旋轉90°后得△A2O1B1在直線x=![]() 上是否存在點K,使得△A2B1K為等腰三角形?若存在,直接寫出點K的坐標;不存在,請說明理由.
上是否存在點K,使得△A2B1K為等腰三角形?若存在,直接寫出點K的坐標;不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組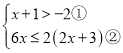
請結合題意填空,完成本題的解答.
(Ⅰ)解不等式①,得____________;
(Ⅱ)解不等式②,得____________;
(Ⅲ)把不等式①和②的解集在數軸上表示出來:
![]()
(Ⅳ)原不等式組的解集為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著中國經濟的快速發展以及科技水平的飛速提高,中國高鐵正迅速崛起.高鐵大大縮短了時空距離,改變了人們的出行方式.如圖,A,B兩地被大山阻隔,由A地到B地需要繞行C地,若打通穿山隧道,建成A,B兩地的直達高鐵,可以縮短從A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后與打通前相比,從A地到B地的路程將約縮短多少公里?(參考數據:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
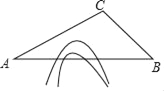
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為配合全市“禁止焚燒秸稈”工作,某學校舉行了“禁止焚燒秸稈,保護環境,從我做起”為主題的演講比賽. 賽后組委會整理參賽同學的成績,并制作了如下不完整的頻數分布表和頻數分布直方圖.
分數段(分數為x分) | 頻數 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
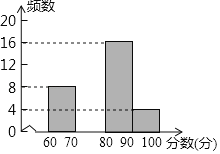
請根據圖表提供的信息,解答下列問題:
(1)表中的a= ,b= ;請補全頻數分布直方圖;
(2)若用扇形統計圖來描述成績分布情況,則分數段70≤x<80對應扇形的圓心角的度數是 ;
(3)競賽成績不低于90分的4名同學中正好有2名男同學,2名女同學. 學校從這4名同學中隨機抽2名同學接受電視臺記者采訪,則正好抽到一名男同學和一名女同學的概率為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com