
【題目】如圖,數軸上每相鄰兩點的相距一個單位長度,點A、B、C、D是這些點中的四個,且對應的位置如圖所示,它們對應的數分別是a,b,c,d.
(1)當ab=﹣1,則d= .
(2)若|d﹣2a|=7,求點C對應的數.
(3)若abcd<0,a+b>0,化簡|a﹣b|﹣|b+c﹣5|﹣|c﹣5|﹣|d﹣a|+|8﹣d|.
![]()
【答案】(1)8;(2)C對應的點就為7或21;(3)﹣8.
【解析】
(1)根據每相鄰兩點的相距一個單位長度,且積為﹣1,可得a,b,進而得d;
(2)由絕對值的含義化簡絕對值,得到d﹣2a=±7,并結合圖形可分類討論求解;
(3)由abcd<0,a<b<c<d,得到a,b,c為負數,d為正數;或者a為負數,b,c,d為正數.又因為a+b>0,可得a為負數,b,c,d為正數;再結合圖形,分析可化簡絕對值,再合并同類項即可.
(1)因為每相鄰兩點的相距一個單位長度,
所以a,b為整數
又ab=﹣1,
所以a=﹣1,b=1,
所以d=8
故答案為:8;
(2)因為|d﹣2a|=7所以d﹣2a=±7;
由圖知:d﹣a=9;
ⅰ.當d﹣2a=7 時,9﹣a=7,則a=2,所以 C 對應的點就為 7;
ⅱ.當d﹣2a=﹣7 時,9﹣a=﹣7,則a=16,所以 C 對應的點就為 21.
(3)因為abcd<0,a<b<c<d,
所以a,b,c為負數,d為正數;或者a為負數,b,c,d為正數.
又因為a+b>0,所以a為負數,b,c,d為正數;
由題與圖可得:﹣1<a<0,1<b<2,4<c<5,8<d<9;
因為a﹣b<0,b+c>0,c﹣5<0,d﹣a>0,8﹣d<0
所以a﹣b﹣b+c﹣5﹣c﹣5﹣d﹣a+8﹣d
=b﹣a﹣(b+c﹣5)+(c﹣5)﹣(d﹣a)﹣(8﹣d )
=b﹣a﹣b﹣c+5+c﹣5﹣d+a﹣8+d
=﹣8.


 優百分課時互動系列答案
優百分課時互動系列答案科目:初中數學 來源: 題型:
【題目】解密數學魔術:魔術師請觀眾心想一個數,然后將這個數按以下步驟操作:![]()
魔術師能立刻說出觀眾想的那個數.
(1)如果小玲想的數是-1,那么她告訴魔術師的結果應該是 ;
(2)如果小明想了一個數計算后,告訴魔術師結果為93,那么魔術師立刻說出小明想的那個數是 ;
(3)觀眾又進行了幾次嘗試,魔術師都能立刻說出他們想的那個數.若設觀眾心想的數為a,請通過計算解密這個魔術的奧妙.
查看答案和解析>>
科目:初中數學 來源: 題型:
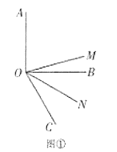
【題目】如圖,![]() 是
是![]() 的平分線,
的平分線,![]() 是
是![]() 的平分線.
的平分線.
(1)如圖①,當![]() 是直角,
是直角,![]() 時,
時,![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
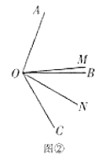
(2)如圖②,當![]() ,
,![]() 時,猜想:
時,猜想:![]() 的度數與
的度數與![]() 的數量關系,并說明理由;
的數量關系,并說明理由;
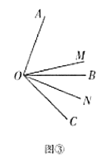
(3)如圖③,當![]() ,
,![]() (
(![]() 為銳角)時,猜想:
為銳角)時,猜想:![]() 的度數與
的度數與![]() ,
,![]() 有怎樣的數量關系?請寫出結論,并說明理由.
有怎樣的數量關系?請寫出結論,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
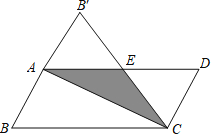
【題目】如圖,在平行四邊形紙片ABCD中,AB=3cm,將紙片沿對角線AC對折,BC邊的對應邊B′C與AD邊交于點E,此時△CDE恰為等邊三角形中,求:
(1)AD的長度.
(2)重疊部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD為△ABC外接圓的直徑,AD⊥BC,垂足為點F,∠ABC的平分線交AD于點E,連接BD,CD.
(1)求證:BD=CD;
(2)請判斷B,E,C三點是否在以D為圓心,以DB為半徑的圓上?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上,老師讓學生尺規作圖畫Rt△ABC,使其斜邊AB=c,一條直角邊BC=a.李明的作法如圖所示,作線段AB使AB=C,以AB為直徑作⊙O,以B為圓心,a為半徑作弧交⊙O于點C,連接AC,△ABC即為所求作的三角形,你認為這種作法中判斷∠ACB是直角的依據是( )
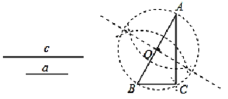
A. 90°的圓周角所對的弦是直徑 B. 直徑所對的圓周角是直角
C. 勾股定理的逆定理 D. 勾股定理
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖將矩形ABCD的四個內角向內折起,恰好拼成一個無縫隙無重疊的四邊形EFGH,EH=12,EF=16,則邊AB的長是( )

A. 8+6![]() B. 12
B. 12![]() C. 19.2D. 20
C. 19.2D. 20
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中央電視臺的“中國詩詞大賽”節目文化品位高,內容豐富,某校初二年級模擬開展“中國詩詞大賽”比賽,對全年級同學成績進行統計后分為“優秀”、“良好”、“一般”、“較差”四個等級,并根據成績繪制成如下兩幅不完整的統計圖,請結合統計圖中的信息,回答下列問題:

(1)扇形統計圖中“優秀”所對應的扇形的圓心角為 度,并將條形統計圖補充完整.
(2)此次比賽有四名同學活動滿分,分別是甲、乙、丙、丁,現從這四名同學中挑選兩名同學參加學校舉行的“中國詩詞大賽”比賽,請用列表法或畫樹狀圖法,求出選中的兩名同學恰好是甲、丁的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一種股票第一天的最高價比開盤價高0.3元,最低價比開盤價低0.2元;第二天的最高價開盤價高0.2元,最低價比開盤價低0.1元;第三天的最高價等于開盤價,最低價比開盤價低0.13元.計算每天最高價與最低價的差,以及這些差的平均值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com