
【題目】在△ABC中,BD是∠ABC的平分線,AD⊥BD,垂足是D.
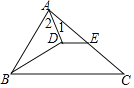
(1)求證:∠2=∠1+∠C;
(2)若ED∥BC,∠ABD=28°,求∠ADE的度數(shù).
【答案】(1)見解析;(2)118°
【解析】
(1)如圖延長(zhǎng)AD交BC于E.證明△BDA≌△BDE(ASA)即可解決問題.
(2)求出∠AEC,再利用平行線的性質(zhì)即可解決問題.
解:(1)如圖延長(zhǎng)AD交BC于E.

∵BD⊥AE,
∴∠BDA=∠BDE=90°,
∵∠ABD=∠EBD,BD=BD,
∴△BDA≌△BDE(ASA),
∴BA=BE,∠2=∠BEA,
∵∠BEA=∠1+∠C,
∴∠2=∠1+∠C.
(2)∵∠ABD=28°,∠BDA=90°,
∴∠2=62°,
∴∠AEB=∠2=62°,
∴∠AEC=180°﹣62°=118°,
∵DE∥EC,
∴∠ADE=∠AEC=118°.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知A(1,5),B(3,-1)兩點(diǎn),在x軸上取一點(diǎn)M,使AM-BM取得最大值時(shí),則M的坐標(biāo)為 ▲
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,直線
,直線![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ,
, ![]() 與
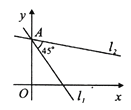
與![]() 在A點(diǎn)相交所形的 夾角為45°(如圖所示),則直線
在A點(diǎn)相交所形的 夾角為45°(如圖所示),則直線![]() 的函數(shù)表達(dá)式為____________.
的函數(shù)表達(dá)式為____________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,![]() 在
在![]() 的正北方向,
的正北方向,![]() 在
在![]() 的正東方向,且
的正東方向,且![]() .某一時(shí)刻,甲車從
.某一時(shí)刻,甲車從![]() 出發(fā),以
出發(fā),以![]() 的速度朝正東方向行駛,與此同時(shí),乙車從
的速度朝正東方向行駛,與此同時(shí),乙車從![]() 出發(fā),以
出發(fā),以![]() 的速度朝正北方向行駛.
的速度朝正北方向行駛.![]() 小時(shí)后,位于點(diǎn)
小時(shí)后,位于點(diǎn)![]() 處的觀察員發(fā)現(xiàn)甲、乙兩車之間的夾角為
處的觀察員發(fā)現(xiàn)甲、乙兩車之間的夾角為![]() ,即
,即![]() ,此時(shí),甲、乙兩人相距的距離為( )
,此時(shí),甲、乙兩人相距的距離為( )

A. 90km B. 50![]() km C. 20
km C. 20![]() km D. 100km
km D. 100km
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商店以固定進(jìn)價(jià)一次性購(gòu)進(jìn)一種商品,3月份按一定售價(jià)銷售,銷售額為2400元,為擴(kuò)大銷量,減少庫(kù)存,4月份在3月份售價(jià)基礎(chǔ)上打9折銷售,結(jié)果銷售量增加30件,銷售額增加840元.
(1)求該商店3月份這種商品的售價(jià)是多少元?
(2)如果該商店3月份銷售這種商品的利潤(rùn)為900元,那么該商店4月份銷售這種商品的利潤(rùn)是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,小明在![]() 處用高
處用高![]() 米(
米(![]() 米)的測(cè)角儀測(cè)得旗桿
米)的測(cè)角儀測(cè)得旗桿![]() 的頂端
的頂端![]() 的仰角為
的仰角為![]() ,再向旗桿方向前進(jìn)
,再向旗桿方向前進(jìn)![]() 米到
米到![]() 處,又測(cè)得旗桿頂端
處,又測(cè)得旗桿頂端![]() 的仰角為
的仰角為![]() ,請(qǐng)求出旗桿
,請(qǐng)求出旗桿![]() 的高度(取
的高度(取![]() ,結(jié)果保留整數(shù))
,結(jié)果保留整數(shù))

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在下面直角坐標(biāo)系中,已知![]() ,
,![]() ,
,![]() 三點(diǎn),其中
三點(diǎn),其中![]() 、
、![]() 、
、![]() 滿足關(guān)系式
滿足關(guān)系式![]() ,
,![]() .
.
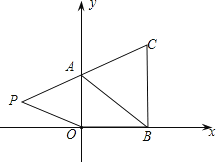
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)如果在第二象限內(nèi)有一點(diǎn)![]() ,請(qǐng)用含
,請(qǐng)用含![]() 的式子表示四邊形
的式子表示四邊形![]() 的面積;
的面積;
(3)在(2)的條件下,是否存在點(diǎn)![]() ,使四邊形
,使四邊形![]() 的面積與
的面積與![]() 的面積相等?若存在,求出點(diǎn)
的面積相等?若存在,求出點(diǎn)![]() 的坐標(biāo),若不存在,請(qǐng)說明理由.
的坐標(biāo),若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
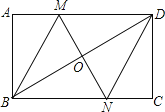
【題目】如圖,在矩形ABCD中,對(duì)角線BD的垂直平分線MN與AD相交于點(diǎn)M,與BD相交于點(diǎn)O,與BC相交于點(diǎn)N,連接BM、DN.
![]() 求證:四邊形BMDN是菱形;
求證:四邊形BMDN是菱形;
![]() 若
若![]() ,
,![]() ,求菱形BMDN的面積和對(duì)角線MN的長(zhǎng).
,求菱形BMDN的面積和對(duì)角線MN的長(zhǎng).
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com