
【題目】問題探究:
新定義:
將一個平面圖形分為面積相等的兩部分的直線叫做該平面圖形的“等積線”,其“等積線”被該平面圖形截得的線段叫做該平面圖形的“等積線段”(例如圓的直徑就是圓的“等積線段”)
解決問題:
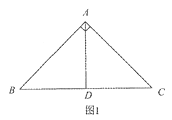
已知在Rt△ABC中,∠BAC=90°,AB=AC=2![]() .
.
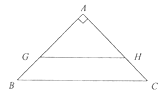
(1)如圖1,若AD⊥BC,垂足為D,則AD是△ABC的一條等積線段,直接寫出AD的長;
(2)在圖2和圖3中,分別畫出一條等積線段,并直接寫出它們的長度. (要求:圖1、圖2和圖3中的等積線段的長度各不相等)
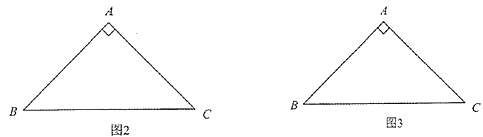
【答案】(1)AD=2;(2)符合題意的圖形見解析,BE=![]() ,GH=2
,GH=2![]()
【解析】試題分析:(1)根據等腰直角三角形的性質,底邊上的高線即可求得;
(2)作中線BE,中線BE即為一條等積線,利用勾股定理即可求得長度;
作GH//BC,GH將Rt△ABC的面積分為相等的兩份,則GH即為一條等積線,根據相似三角形的性質即可求得長度.
試題解析:(1)在Rt△ADC中,
∵AC=2![]() ,∠C=45°,
,∠C=45°,
∴AD=2;
(2)符合題意的圖形如下所示:
E為AC中點,則有AE=![]() ,
,
在Rt△ABE中,根據勾股定理可得BE=![]() =
=![]() ;
;
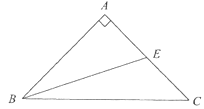
GH∥BC,S△AGH=![]() S△ABC,
S△ABC,
∵GH//BC,∴△AGH∽△ABC,
∴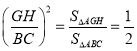 ,
,
∵∠A=90°,AB=AC=![]() ,∴BC=
,∴BC=![]() =4,
=4,
∴![]() ,
,
∴GH=2![]() .
.


科目:初中數學 來源: 題型:
【題目】2019年4月23日,第24個世界讀書日,為了推進中華傳統文化教育,營造濃郁的讀書氛圍,我區某學校舉辦了“讓讀書成為習慣,讓書香飄滿校園”主題活動,為此特為每個班級訂購了一批新的圖書,初一年級兩個班訂購圖書情況如下表:

老舍文集(套) | 四大名善(套) | 總表用(元) | |
初一(1)班 | 4 | 2 | 80 |
初一(2)班 | 2 | 3 | 520 |
(1)求老舍文集和四大名著每套各是多少元;
(2)學校準備再購買老舍文集和四大名著共10套,總費用不超過700元。問學校有哪幾種購買方案。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD,AF分別為△ABC的中線和高,BE為△ABD的角平分線.
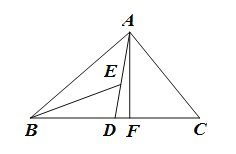
(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面積為40,BD=5,求AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
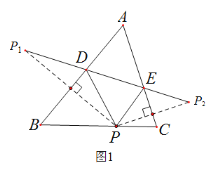
【題目】(1)如圖1,在△ABC中,∠A![]() ,P是BC邊上的一點,
,P是BC邊上的一點,![]() ,
,![]() 是點P關于AB、AC的對稱點,連結
是點P關于AB、AC的對稱點,連結![]() ,分別交AB、AC于點D、E.
,分別交AB、AC于點D、E.
①若![]() ,求
,求![]() 的度數;
的度數;
②請直接寫出∠A與![]() 的數量關系:___________________________;
的數量關系:___________________________;
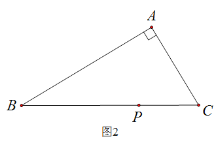
(2)如圖2,在△ABC中,若∠BAC![]() ,用三角板作出點P關于AB、AC的對稱點
,用三角板作出點P關于AB、AC的對稱點![]() 、
、![]() ,(不寫作法,保留作圖痕跡),試判斷點
,(不寫作法,保留作圖痕跡),試判斷點![]() ,
,![]() 與點A是否在同一直線上,并說明理由.
與點A是否在同一直線上,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一位農民帶上若干千克自產的土豆進城出售.為了方便,他帶了一些零錢備用,按市場價售出一些后,又降價出售,售出的土豆千克數與他手中持有的錢數(含備用零錢)的關系,如圖,結合圖象回答下列問題:
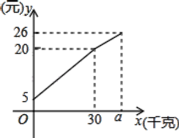
(1)農民自帶的零錢是多少?
(2)求出降價前每千克的土豆價格是多少?
(3)降價后他按每千克0.4元將剩余土豆售完,這時他手中的錢(含備用零錢)是26元,試問他一共帶了多少千克土豆?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)求一次函數y=2x-2的圖象l1與y=![]() x-1的圖象l2的交點P的坐標.
x-1的圖象l2的交點P的坐標.
(2)求直線![]() 與
與![]() 軸交點A的坐標; 求直線
軸交點A的坐標; 求直線![]() 與x軸的交點B的坐標;
與x軸的交點B的坐標;
(3)求由三點P、A、B圍成的三角形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,E是AB邊上一點,且∠A=∠EDF=60°,有下列結論:①AE=BF;②△DEF是等邊三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中結論正確的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校環保志愿者協會對該市城區的空氣質量進行調查,從全年365天中隨機抽取了80天的空氣質量指數(AQI)數據,繪制出三幅不完整的統計圖表.請根據圖表中提供的信息解答下列問題:
AQI指數 | 質量等級 | 天數(天) |
0﹣50 | 優 | m |
51﹣100 | 良 | 44 |
101﹣150 | 輕度污染 | n |
151﹣200 | 中度污染 | 4 |
201﹣300 | 重度污染 | 2 |
300以上 | 嚴重污染 | 2 |
(1 )統計表中m= ,n= .扇形統計圖中,空氣質量等級為“良”的天數占 %;
(2)補全條形統計圖,并通過計算估計該市城區全年空氣質量等級為“優”和“良”的天數共多少天?
(3)據調查,嚴重污染的2天發生在春節期間,燃放煙花爆竹成為空氣污染的一個重要原因,據此,請你提出一條合理化建議.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.動點M以每秒1個單位長的速度,從點A沿線段AB向點B運動;同時點P以相同的速度,從點C沿折線C-D-A向點A運動.當點M到達點B時,兩點同時停止運動.過點M作直線l∥AD,與線段CD的交點為E,與折線A-C-B的交點為Q.點M運動的時間為t(秒).
(1)當t=0.5時,求線段QM的長;
(2)當M在AB上運動時,是否可以使得以C、P、Q為頂點的三角形為直角三角形?若可以,請求t的值;若不可以,請說明理由.
(3)當t>2時,連接PQ交線段AC于點R.請探究![]() 是否為定值,若是,試求這個定值;若不是,請說明理由.
是否為定值,若是,試求這個定值;若不是,請說明理由.



查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com