
【題目】已知,如圖,在矩形ABCD中,AB=8,BC=x(0<x≤8),點E在邊CD上,且CE=CB,以AE為對角線作正方形AGEF.設正方形AGEF的面積y.
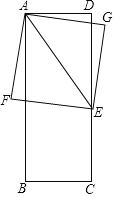
(1)當點F在矩形ABCD的邊上時,x= .
(2)求y與x的函數關系式及y的取值范圍.
(3)當矩形ABCD的一條邊將正方形AGEF的面積分為1:3兩部分時,直接寫出x的值.
【答案】(1)4;(2)y=x2﹣8x+32=(x﹣4)2+16,16≤y≤32;(3)滿足條件的x的值為2或6.
【解析】
(1)點F在矩形ABCD的邊上時,AF=EF=FG=BC,利用正方形的性質解決問題即可.
(2)根據y=![]() AE2=
AE2=![]() (AD2+DE2),計算即可.
(AD2+DE2),計算即可.
(3)分兩種情形:①如圖1中,設CD交AG于Q,當AQ=GQ時,長方形ABCD的邊CD將正方形AFEG的面積分成1:3兩部分.②如圖2中,設AD交EG于Q,當GQ=EG時,長方形ABCD的邊AD將正方形AFEG的面積分成1:3兩部分.
解:(1)點F在矩形ABCD的邊上時,AF=EF=FG=BC,
∵EC=BC,
∴AF=FB=4,
∴BC=EC=BF=4,
故答案為4.
(2)y=![]() AE2=
AE2=![]() (AD2+DE2)=
(AD2+DE2)=![]() [x2+(8﹣x)2]=x2﹣8x+32=(x﹣4)2+16.
[x2+(8﹣x)2]=x2﹣8x+32=(x﹣4)2+16.
∵0<x≤8,
∴16≤y≤32.
(3)①如圖1中,設CD交AG于Q,當AQ=GQ時,長方形ABCD的邊CD將正方形AFEG的面積分成1:3兩部分.
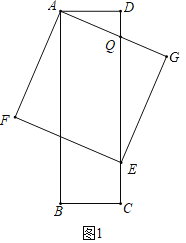
則∵tan∠QEG=tan∠QAD,
∴![]() =
=![]() =
=![]() ,
,
∵AD=BC=x,
∴DQ=![]() x,AQ=GQ=
x,AQ=GQ=![]() xEG=
xEG=![]() x,
x,
∴EQ=![]() x,
x,
∵DQ+QE+CE=8,
∴![]() x+
x+![]() x+x=8,
x+x=8,
∴x=2.
②如圖2中,設AD交EG于Q,當GQ=EG時,長方形ABCD的邊AD將正方形AFEG的面積分成1:3兩部分.
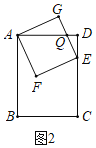
設DQ=m,同法可得DE=2m,QE=GQ=![]() m,AQ=5m,
m,AQ=5m,
∴6m=x,
∴DE=![]() ,
,
∵DE+CE=8,
∴![]() x+x=8,
x+x=8,
∴x=6,
∴滿足條件的x的值為2或6.


科目:初中數學 來源: 題型:
【題目】某果農在其承包的果園中種植了60棵桔子樹,每棵桔子樹的產量是100kg,果農想增加桔子樹的棵數來增產,但增加果樹會導致每棵樹的光照減少,使得單棵果樹產量減少,試驗發現每增加1棵桔子樹,單棵桔子樹的產量減少0.5kg.
(1)在投入成本最低的情況下,增加多少棵桔子樹時,可以使果園總產量達到6650kg?
(2)設增加x棵桔子樹,考慮實際增加桔子樹的情況,10≤x≤40,請你計算一下,果園總產量最多為多少kg,最少為多少kg?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點H,點F是![]() 上一點,連接AF交CD的延長線于點E.
上一點,連接AF交CD的延長線于點E.
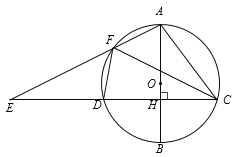
(1)求證:△AFC∽△ACE;
(2)若AC=5,DC=6,當點F為![]() 的中點時,求AF的值.
的中點時,求AF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
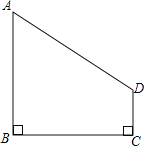
【題目】在四邊形ABCD中,∠B=∠C=90°,若AB=4,BC=4,CD=1,問:在BC上是否存在點P,使得AP⊥PD?若存在,求出BP的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四張大小、形狀都相同的卡片上分別寫有數字1,2,3,4,把它們放入不透明的盒子中搖勻.
(1)從中隨機抽出1張卡片,抽出的卡片上的數字恰好是偶數的概率為 .
(2)從中隨機抽出1張卡片,記錄數字后放回搖勻,再抽出一張卡片,記錄數字.用樹狀圖或列表法求兩次抽出的卡片上的數字恰好是兩個相鄰整數的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有三張形狀大小完全相同的牌,正面分別標有數字2,3,5.將三張牌背面朝上,洗勻后放在桌子上.
(1)從中任取一張,求取到偶數的概率.
(2)甲、乙兩人進行摸牌游戲.
①甲從中隨機抽取一張牌,記錄數字后放回洗勻,乙再隨機抽取一張.請用列表法或畫樹狀圖的方法,求兩人抽取相同數字的概率;
②若兩人抽取的數字和為2的倍數,則甲獲勝;若抽取的數字和為5的倍數,則乙獲勝.這個游戲公平嗎?請用概率的知識加以解釋.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O為坐標原點,點A(3,0),B(3,4).

(1)畫出△AOB繞原點O逆時針旋轉90°得到的△A'OB',并寫出點A',B'的坐標;
(2)求線段AB在上述旋轉過程中掃過的區域面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,以
,以![]() 為直徑作
為直徑作![]() ,點D在
,點D在![]() 上,
上,![]() ,
,![]() ,垂足為點E,
,垂足為點E,![]() 與
與![]() 和
和![]() 分別交于點M、F.連接
分別交于點M、F.連接![]() 、
、![]() 、
、![]() .
.

(1)證明:![]() 是
是![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,求
,求![]() 的半徑長;
的半徑長;
(3)在(2)的條件下,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com