Question

在Rt△ABC中，∠C=90°，AC=3，BC=4，以C為圓心，r為半徑的圓與AB有怎樣的位置關系？為什么？
（1）r=2； （2）r=2.4； （3）r=3．

Answer 1

【答案】分析：先根據題意畫出圖形，由勾股定理求出AB的長，作CD⊥AB于D，利用三角形的面積公式得出CD的長，再根據r的值與CD的大小進行解答．
解答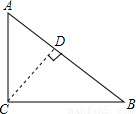：解：作CD⊥AB于D，
在直角三角形ABC中，根據勾股定理得AB=5，則
CD==2.4；
（1）當r=2時，2.4＞2，直線和圓相離；
②當r=2.4時，直線和圓相切；
③當r=3時，2.4＜3，直線和圓相交．
點評：本題考查的是直線與圓的位置關系，即設⊙O的半徑為r，圓心O到直線l的距離為d，
①若直線l和⊙O相交，則d＜r；
②若直線l和⊙O相切，則d=r；
③若直線l和⊙O相離，則d＞r．