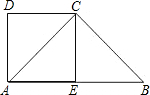
已知：梯形ABCD中，AD∥BC，AD=1，BD過梯形的高AE的中點F，且BD⊥DC，設AE=h，BC=a．
（1）用含字母h的代數式表示a；
（2）若a、h是關于x的一元二次方程3x2-3（m+2）x+10m=0的兩根，求sin∠DBC的值．
分析：（1）首先由Rt△AFD≌Rt△EFB，可得BF=FD，BE=1；且EF=
；且BD=BF；進而可用h表示出BD，BF的長，再根據Rt△BEF∽Rt△BDC，可得
=；代入h的關系與BC=a可得答案；
（2）由根與系數的關系可得a+h=m+2，ah=
；結合（1）的結論，可得a，h的值，進而可得CD的長，再根據三角函數的定義，可得答案．
解答：
解：（1）根據題意，AD∥BC，且AF=EF；
易得Rt△AFD≌Rt△EFB，故BF=FD，BE=1；且EF=
；
由勾股定理可得：BF=
；又可得AD=2AF；
Rt△BEF與Rt△BDC中，有∠BEF=∠BDC=90°，∠B=∠B；
故Rt△BEF∽Rt△BDC，進而可得
=；
化簡可得：a=2（1+
）；即a=2+
．
（2）若a、h是關于x的一元二次方程3x
2-3（m+2）x+10m=0的兩根，
則a+h=m+2，ah=
；
又有a=2+
；解可得a=20，h=6；
DC=
=16；
易得sin∠DBC=
=
．
點評：本題考查梯形，菱形、直角三角形的相關知識．解決此類題要懂得用梯形的常用輔助線，把梯形分割為菱形和直角三角形，從而由菱形和直角三角形的性質來求解．
已知直角梯形ABCD中，AB∥DC，∠DAB=90°，AD=DC=
11、已知直角梯形ABCD中，AD∥BC，∠BCD=90°，BC=CD=2AD，E、F分別是BC、CD邊的中點，連接BF、DE交于點P，連接CP并延長交AB于點Q，連接AF．則下列結論不正確的是（ ）
如圖所示，已知等腰梯形ABCD中，AD∥BC，AB=DC，AC與BD相交于點O．請在圖中找出一對全等的三角形，并加以證明．
如圖，已知等腰梯形ABCD中，AD∥BC，BD⊥DC，∠DBC=
如圖，已知在梯形ABCD中，DC∥AB，AD=BC，∠A=60°，BD平分∠ABC，若AD=1，則對角線BD的長是（ ）