
【題目】若二次函數y=ax2+bx+c(a<0)的圖象如圖所示,且關于x的方程ax2+bx+c=k有兩個不相等的實根,則常數k的取值范圍是( )
A.0<k<4
B.﹣3<k<1
C.k<﹣3或k>1
D.k<4
【答案】D
【解析】解:由圖象可知,拋物線的對稱軸為x=﹣1,
∴頂點坐標為(﹣1,4),
設拋物線的解析式為:y=a(x+1)2+4,
把(1,0)代入解析式得,a=﹣1,
∴解析式為:y=﹣x2﹣2x+3,
方程=﹣x2﹣2x+3=k有兩個不相等的實根,
△=4+12﹣4k>0,
解得:k<4.
所以答案是:D.
【考點精析】解答此題的關鍵在于理解求根公式的相關知識,掌握根的判別式△=b2-4ac,這里可以分為3種情況:1、當△>0時,一元二次方程有2個不相等的實數根2、當△=0時,一元二次方程有2個相同的實數根3、當△<0時,一元二次方程沒有實數根,以及對一元一次不等式的解法的理解,了解步驟:①去分母;②去括號;③移項;④合并同類項; ⑤系數化為1(特別要注意不等號方向改變的問題).


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】在四邊形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,點P從點A出發,沿折線ABCD方向以3cm/s的速度勻速運動;點Q從點D出發,沿線段DC方向以2cm/s的速度勻速運動. 已知兩點同時出發,當一個點到達終點時,另一點也停止運動,設運動時間為t(s).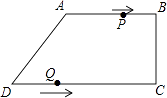
(1)求CD的長;
(2)當四邊形PBQD為平行四邊形時,求四邊形PBQD的周長;
(3)在點P、Q的運動過程中,是否存在某一時刻,使得△BPQ的面積為20cm2?若存在,請求出所有滿足條件的t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】方格紙中每個小方格都是邊長為1個單位長度的正方形,在平面直角坐標系中,已知![]() ,
,![]() .
.

(1)在圖中描出A,B兩點的位置,并連結![]() ,
,![]() ,
,![]() ;
;
(2)把![]() 向右平移4個單位,再向上平移2個單位,得到
向右平移4個單位,再向上平移2個單位,得到![]() ,在圖中畫出
,在圖中畫出![]() ,并標注出
,并標注出![]() ,
,![]() ,
,![]() 的坐標;
的坐標;
(3)求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,![]() ,點
,點![]() 在射線
在射線![]() 上,
上,![]() .
.

(1)如圖 1,若![]() ,求
,求![]() 的度數;
的度數;
(2)把“![]() °”改為“
°”改為“![]() ”,射線
”,射線![]() 沿射線
沿射線![]() 平移,得到
平移,得到![]() ,其它條件不變(如 圖 2 所示),探究
,其它條件不變(如 圖 2 所示),探究![]() 的數量關系;
的數量關系;
(3)在(2)的條件下,作![]() ,垂足為
,垂足為![]() ,與
,與![]() 的角平分線
的角平分線![]() 交于點
交于點![]() ,若
,若![]() , 用含 α 的式子表示
, 用含 α 的式子表示![]() (直接寫出答案).
(直接寫出答案).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線AB和CD交于點O,∠AOC的度數為x,∠BOE=90°,OF平分∠AOD.
(1)當x=19°48′,求∠EOC與∠FOD的度數.
(2)當x=60°,射線OE、OF分別以10°/s,4°/s的速度同時繞點O順時針轉動,求當射線OE與射線OF重合時至少需要多少時間?
(3)當x=60°,射線OE以10°/s的速度繞點O順時針轉動,同時射線OF也以4°/s的速度繞點O逆時針轉動,當射線OE轉動一周時射線OF也停止轉動.射線OE在轉動一周的過程中當∠EOF=90°時,求射線OE轉動的時間.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖 1 所示,△ ABC 和△ AEF 為等邊三角形,點 E 在△ ABC 內部,且 E 到點 A、B、C 的距離分別為 3、4、5,求∠AEB 的度數.
(2)如圖 2,在△ ABC 中,∠CAB=90°,AB=AC,M、N 為 BC 上的兩點,且∠MAN=45°,MN2 與 NC2+BM2 有何關系?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】寧安市與哈爾濱市兩地相距360千米.甲車在寧安市,乙車在哈爾濱市,兩車同時出發,相向而行,在A地相遇.為節約費用(兩車相遇并換貨后,均需按原路返回出發地),兩車換貨后,甲車立即按原路返回寧安市.設每車在行駛過程中速度保持不變,兩車間距離y(千米)與時間x(小時)的函數關系如圖所示.根據所提供的信息,回答下列問題:
(1)求甲、乙兩車的速度;(2)說明從兩車開始出發到5小時這段時間乙車的運動狀態.

查看答案和解析>>
科目:初中數學 來源: 題型:
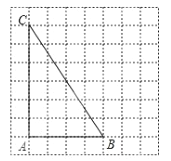
【題目】作圖題:如圖所示是每一個小方格都是邊長為1的正方形網格,
(1)利用網格線作圖:
①在![]() 上找一點P,使點P到
上找一點P,使點P到![]() 和
和![]() 的距離相等;
的距離相等;
②在射線![]() 上找一點Q,使
上找一點Q,使![]() .
.
(2)在(1)中連接![]() 與
與![]() ,試說明
,試說明![]() 是直角三角形.
是直角三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系中,點A、B的坐標分別是(a,0),(b,0)且![]() +|b-2|=0.
+|b-2|=0.
(1)求a、b的值;
(2)在y軸上是否存在點C,使三角形ABC的面積是12?若存在,求出點C的坐標;若不存在,請說明理由.
(3)已知點P是y軸正半軸上一點,且到x軸的距離為3,若點P沿平行于x軸的負半軸方向以每秒1個單位長度平移至點Q,當運動時間t為多少秒時,四邊形ABPQ的面積S為15個平方單位?寫出此時點Q的坐標. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com