
【題目】請閱讀下面材料,并回答所提出的問題.三角形內角平分線定理:三角形的內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例.
已知:如圖,△ABC中, AD是角平分線.
求證: ![]() .
.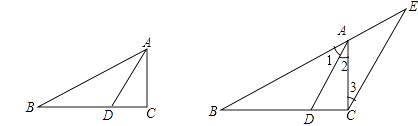
證明:過C作CE∥DA,交BA的延長線于E.
∴ ![]() . ①
. ①![]() AD是角平分線,
AD是角平分線,
∴ ![]() .
.![]()
![]() .
.![]() . ②
. ②
又 ![]() ,
,![]() . ③
. ③![]()
![]() .
.
(1)上述證明過程中,步驟①②③處的理由是什么?(寫出兩條即可)
(2)用三角形內角平分線定理解答:已知,△ABC中,AD是角平分線,AB=7cm,AC=4cm,BC=6cm,求BD的長;
(3)我們知道如果兩個三角形的高相等,那么它們面積的比就等于底的比.請你通過研究△ABD和△ACD面積的比來證明三角形內角平分線定理.
【答案】
(1)解:證明過程中用到的定理有:
①平行線的性質定理;
②等腰三角形的判定定理;
③平行線分線段成比例定理
(2)解:∵AD是角平分線,
∴ ![]() ,
,
又∵AB=7cm,AC=4cm,BC=6cm,
∴ ![]() ,
,
∴BD= ![]() (cm)
(cm)
(3)解:∵△ABD和△ACD的高相等,
可得:△ABD和△ACD面積的比= 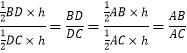 ,
,
可得: ![]()
【解析】(1)利用“平行線的性質定理;等腰三角形的判定定理;平行線分線段成比例定理”可填出答案;(2)學會應用(1)的結論,構造比例式求線段;(3)利用面積法,再結合角平分線性質定理可構造兩個比例式,證得結論.
【考點精析】利用三角形的面積和角平分線的性質定理對題目進行判斷即可得到答案,需要熟知三角形的面積=1/2×底×高;定理1:在角的平分線上的點到這個角的兩邊的距離相等; 定理2:一個角的兩邊的距離相等的點,在這個角的平分線上.


 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,D、E分別是AB、BC的中點,F在CA延長線上,∠FDA=∠B,AC=6,AB=8,則四邊形AEDF的周長為( )
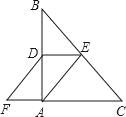
A. 16 B. 20 C. 18 D. 22
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某小區在規劃改造期間,欲拆除小區廣場邊的一根電線桿AB,已知距電線桿AB水平距離14米處是觀景臺,即BD=14米,該觀景臺的坡面CD的坡角∠CDF的正切值為2,觀景臺的高CF為2米,在坡頂C處測得電線桿頂端A的仰角為30°,D、E之間是寬2米的人行道,如果以點B為圓心,以AB長為半徑的圓形區域為危險區域.請你通過計算說明在拆除電線桿AB時,人行道是否在危險區域內?( ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1, 在 ![]() 中,
中, ![]() ,
, ![]() .點O是BC的中點,點D沿B→A→C方向從B運動到C.設點D經過的路徑長為
.點O是BC的中點,點D沿B→A→C方向從B運動到C.設點D經過的路徑長為 ![]() ,圖1中某條線段的長為y,若表示y與x的函數關系的圖象大致如圖2所示,則這條線段可能是圖1中的( )
,圖1中某條線段的長為y,若表示y與x的函數關系的圖象大致如圖2所示,則這條線段可能是圖1中的( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】石頭剪子布,又稱“猜丁殼”,是一種起源于中國流傳多年的猜拳游戲.游戲時的各方每次用一只手做“石頭”、“剪刀”、“布”三種手勢中的一種,規定“石頭”勝“剪刀”、“剪刀”勝“布”、“布”勝“石頭” .兩人游戲時,若出現相同手勢,則不分勝負游戲繼續,直到分出勝負,游戲結束.三人游戲時,若三種手勢都相同或都不相同,則不分勝負游戲繼續;若出現兩人手勢相同,則視為一種手勢與第三人所出手勢進行對決,此時,參照兩人游戲規則.例如甲、乙二人同時出石頭,丙出剪刀,則甲、乙獲勝.假定甲、乙、丙三人每次都是隨機地做這三種手勢,那么:
(1)直接寫出一次游戲中甲、乙兩人出第一次手勢時,不分勝負的概率;
(2)請你畫出樹狀圖求出一次游戲中甲、乙、丙三人出第一次手勢時, 不分勝負的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在筆直的鐵路上A、B兩點相距25km,C、D為兩村莊,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,現要在AB上建一個中轉站E,使得C、D兩村到E站的距離相等.求E應建在距A多遠處?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D,E分別在△ABC的AB,AC邊上,增加下列條件中的一個:①∠AED=∠B,②∠ADE=∠C,③ ![]()
![]() ,④
,④ ![]()
![]() , ⑤
, ⑤ ![]()
![]() ,使△ADE與△ACB一定相似的有( )
,使△ADE與△ACB一定相似的有( )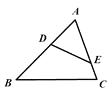
A.①②④
B.②④⑤
C.①②③④
D.①②③⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在Rt△ABC中,∠C=90°.將△ABC繞點C逆時針旋轉得到△A’B’C,旋轉角為 ![]() ,且0°<
,且0°< ![]() <180°.在旋轉過程中,點B’可以恰好落在AB的中點處,如圖②.
<180°.在旋轉過程中,點B’可以恰好落在AB的中點處,如圖②.
(1)求∠A的度數;
(2)當點C到AA’的距離等于AC的一半時,求 ![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:一組數據x1,x2,x3,x4,x5的平均數是2,方差是![]() ,那么另一組數據3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均數和方差分別是( )
,那么另一組數據3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均數和方差分別是( )
A. 2,![]() B. 2,1 C. 4,
B. 2,1 C. 4,![]() D. 4,3
D. 4,3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com