Question

敘述并證明三角形內角和定理．
要求寫出定理、已知、求證，畫出圖形，并寫出證明過程．
定理：________
已知：________
求證：________
證明：

Answer 1

三角形的內角和是180°    △ABC的三個內角分別為∠A，∠B，∠C    ∠A+∠B+∠C=180°
分析：欲證明三角形的三個內角的和為180°，可以把三角形三個角轉移到一個平角上，利用平角的性質解答．
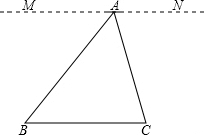
解答：定理：三角形的內角和是180°；
已知：△ABC的三個內角分別為∠A，∠B，∠C；
求證：∠A+∠B+∠C=180°．
證明：過點A作直線MN，使MN∥BC．
∵MN∥BC，
∴∠B=∠MAB，∠C=∠NAC（兩直線平行，內錯角相等）
∵∠MAB+∠NAC+∠BAC=180°（平角定義）
∴∠B+∠C+∠BAC=180°（等量代換）
即∠A+∠B+∠C=180°．
點評：本題考查的是三角形內角和定理，即三角形的內角和是180°．