【題目】已知，如圖在直角坐標系中，點A在y軸上，BC⊥x軸于點C，點A關于直線OB的對稱點D恰好在BC上，點E與點O關于直線BC對稱，∠OBC=35°，則∠OED的度數為（ ）
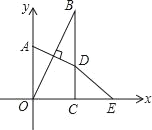
A.10°B.20°C.30°D.35°
【答案】B
【解析】
先根據平行線的性質求出∠AOB的度數，由直角三角形的性質得出∠BOC的度數，再根據點A關于直線OB的對稱點D恰好在BC上得出OB是線段AD的垂直平分線，故可得出∠BOD的度數，進而得出∠DOC的度數，由點E與點O關于直線BC對稱可知BC是OE的垂直平分線，故可得出∠DOC=∠OED．
解：連接OD，
∵BC⊥x軸于點C，∠OBC=35°，
∴∠AOB=∠OBC=35°，∠BOC=90°-35°=55°．
∵點A關于直線OB的對稱點D恰好在BC上，
∴OB是線段AD的垂直平分線，
∴∠BOD=∠AOB=35°，
∴∠DOC=∠BOC-∠BOD=55°-35°=20°．
∵點E與點O關于直線BC對稱，
∴BC是OE的垂直平分線，
∴∠DOC=∠OED=20°．
故選：B．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，△OAB是邊長為2的等邊三角形過點A的直線
與
軸交于點E，
（1）求點E坐標。
（2）求過A，O，E三點的拋物線表達式。
（3）若P是（2）中求出的拋物線AE段上的一動點（不與A、E重合），設四邊形OAPE的面積為S，求S的最大值。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，BA＝BC，D在邊CB上，且DB＝DA＝AC
（1）填空：如圖1，∠B＝ °，∠C＝ °；
（2）如圖2，若M為線段BC上的點，過M作MH⊥AD，交AD的延長線于點H，分別交直線AB、AC與點N、E．
①求證：△ANE是等腰三角形；
②線段BN、CE、CD之間的數量關系是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】將一把三角尺放在邊長為2的正方形ABCD上(正方形四個內角為90°,四邊都相等),并使它的直角頂點P在對角線AC上滑動,直角的一邊始終經過點B,另一邊與射線DC交于點Q。
探究:(1)當點Q在邊CD 上時,線段PQ 與線段PB之間有怎樣的大小關系?試證明你觀察得到結論；
(2)當點Q在邊CD 上時,如果四邊形 PBCQ 的面積為1，求AP長度；
(3)當點P在線段AC 上滑動時,△PCQ 是否可能成為等腰三角形?如果可能,指出所有能使△PCQ 成為等腰三角形的點Q的位置,并求出相應的AP的長；如果不可能,試說明理由。
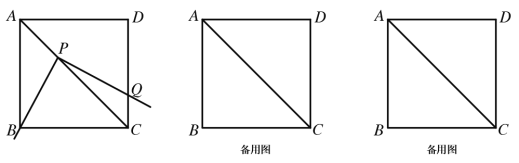
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=1，△ABC繞點C順時針旋轉一定角度得到△DEC，點D恰好落在AB邊上，連接AE. 求：
（1）旋轉角的度數；
（2）AE的長度.
查看答案和解析>>
科目：初中數學 來源： 題型：
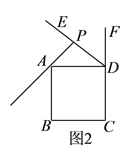
【題目】在正方形
中，
為正方形的外角
的角平分線，點
在線段
上，過點作
于點
，連接
，過點
作
于點
，交射線
于點
．
（
）如圖1，若點與點
重合．
①依題意補全圖1．
②判斷
與
的數量關系并加以證明．
（
）如圖2，若點恰好在線段
上，正方形的邊長為，請寫出求
長的思路（可以不寫出計算結果）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，CD為AB邊上的高，AD＝8，CD＝4，BD＝3．動點P從點A出發，沿射線AB運動，速度為1個單位/秒，運動時間為t秒．
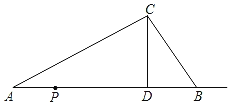
（1）當t為何值時，△PDC≌△BDC；
（2）當t為何值時，△PBC是等腰三角形？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
