
【題目】如圖,拋物線![]() 交
交![]() 軸于點
軸于點![]() 和
和![]() ,交
,交![]() 軸于點
軸于點![]() ,拋物線的頂點為
,拋物線的頂點為![]() ,下列四個判斷:①當
,下列四個判斷:①當![]() 時,
時,![]() ;②若
;②若![]() ,則
,則![]() ;③拋物線上有兩點
;③拋物線上有兩點![]() 和
和![]() ,若
,若![]() ,且
,且![]() ,則
,則![]() ;④點
;④點![]() 關于拋物線對稱軸的對稱點為
關于拋物線對稱軸的對稱點為![]() ,點
,點![]() 、
、![]() 分別在
分別在![]() 軸和
軸和![]() 軸上,當
軸上,當![]() 時,四邊形
時,四邊形![]() 周長的最小值為
周長的最小值為![]() .其中,判斷正確的序號是( )
.其中,判斷正確的序號是( )
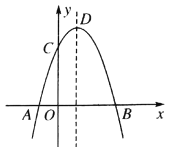
A. ①②B. ②③C.
【答案】B
【解析】
①根據二次函數所過象限,判斷出y的符號;
②根據A、B關于對稱軸對稱,求出b的值;
③根據![]() >1,得到x1<1<x2,從而得到Q點距離對稱軸較遠,進而判斷出y1>y2;
>1,得到x1<1<x2,從而得到Q點距離對稱軸較遠,進而判斷出y1>y2;
④作D關于y軸的對稱點D′,E關于x軸的對稱點E′,連接D′E′,D′E′與DE的和即為四邊形EDFG周長的最小值.求出D、E、D′、E′的坐標即可解答.
①當x>0時,函數圖象過一四象限,當0<x<b時,y>0;當x>b時,y<0,故本選項錯誤;
②二次函數對稱軸為x=-![]() =1,當a=-1時有
=1,當a=-1時有![]() =1,解得b=3,故本選項正確;
=1,解得b=3,故本選項正確;
③∵x1+x2>2,
∴![]() >1,
>1,
又∵x1-1<1<x2-1,
∴Q點距離對稱軸較遠,
∴y1>y2,故本選項正確;
④如圖,作D關于y軸的對稱點D′,E關于x軸的對稱點E′,
連接D′E′,D′E′與DE的和即為四邊形EDFG周長的最小值.
當m=2時,二次函數為y=-x2+2x+3,頂點縱坐標為y=-1+2+3=4,D為(1,4),則D′為(-1,4);C點坐標為C(0,3);則E為(2,3),E′為(2,-3);
則DE=![]() .
.
∴四邊形EDFG周長的最小值為![]() ,故本選項錯誤.
,故本選項錯誤.
正確的有2個.
故選:B.


科目:初中數學 來源: 題型:
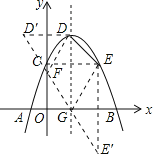
【題目】在如圖所示的半圓中,P是直徑AB上一動點,過點P作PC⊥AB于點P,交半圓于點C,連接AC.已知AB=6cm,設A,P兩點間的距離為xcm,P,C兩點間的距離為y1cm,A,C兩點間的距離為y2cm.
小聰根據學習函數的經驗,分別對函數y1,y2隨自變量x的變化而變化的規律進行了探究.
下面是小聰的探究過程,請補充完整:
(1)按照下表中自變量x的值進行取點、畫圖、測量,分別得到了y1,y2與x的幾組對應值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.24 | 2.83 | 2.83 | 2.24 | 0 | |
y2/cm | 0 | 2.45 | 3.46 | 4.24 | 4.90 | 5.48 | 6 |
(2)在同一平面直角坐標系xOy中,描出補全后的表中各組數值所對應的點(x,y1),(x,y2),并畫出函數y1,y2的圖象;
(3)結合函數圖象,解決問題:當△APC有一個角是30°時,AP的長度約為 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知反比例函數![]() 的圖象經過點
的圖象經過點![]() ,點
,點![]() 與點
與點![]() 關于原點對稱,一次函數
關于原點對稱,一次函數![]() 的圖象經過點
的圖象經過點![]() ,交反比例函數圖象于點
,交反比例函數圖象于點![]() ,連接
,連接![]() .
.
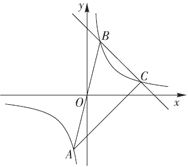
(1)求反比例函數與一次函數的表達式;
(2)求![]() 的面積;
的面積;
(3)直接寫出當![]() 時,
時,![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
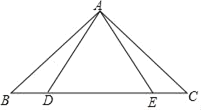
【題目】如圖,在△ABC中,∠B=∠C=40°,點D、點E分別從點B、點C同時出發,在線段BC上作等速運動,到達C點、B點后運動停止.
(1)求證:△ABE≌△ACD;
(2)若AB=BE,求∠DAE的度數;
拓展:若△ABD的外心在其內部時,求∠BDA的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是放在水平地面上的一把椅子的側面圖,椅子高為AC,椅面寬為BE,椅腳高為ED,且AC⊥BE,AC⊥CD,AC∥ED.從點A測得點D、E的俯角分別為64°和53°.已知ED=35cm,求椅子高AC約為多少?
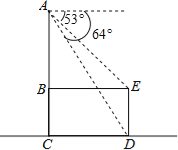
(參考數據:tan53°≈![]() ,sin53°≈
,sin53°≈![]() ,tan64°≈2,sin64°≈
,tan64°≈2,sin64°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A是反比例函數y=![]() 圖象上一點,過點A作x軸的平行線交反比例函數y=﹣
圖象上一點,過點A作x軸的平行線交反比例函數y=﹣![]() 的圖象于點B,點C在x軸上,且S△ABC=
的圖象于點B,點C在x軸上,且S△ABC=![]() ,則k=( )
,則k=( )
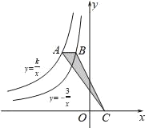
A. 6B. ﹣6C. ![]() D. ﹣
D. ﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
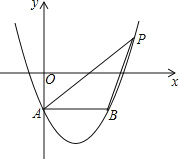
【題目】如圖,在平面直角坐標系中,拋物線y=x2-2x-1交y軸于點A,過點A作AB∥x軸交拋物線于點B,點P在拋物線上,連結PA、PB,若點P關于x軸的對稱點恰好落在直線AB上,則△ABP的面積是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在趣味運動會“定點投籃”項目中,我校七年級八個班的投籃成績![]() 單位:個
單位:個![]() 分別為:24,20,19,20,22,23,20,
分別為:24,20,19,20,22,23,20,![]() 則這組數據中的眾數和中位數分別是
則這組數據中的眾數和中位數分別是![]()
![]()
A. 22個、20個 B. 22個、21個 C. 20個、21個 D. 20個、22個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com