
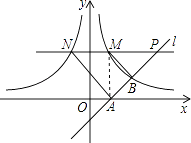
【題目】如圖,已知直線l經過點A(1,0),與雙曲線y= ![]() (x>0)交于點B(2,1).過點P(p,p﹣1)(p>1)作x軸的平行線分別交雙曲線y=
(x>0)交于點B(2,1).過點P(p,p﹣1)(p>1)作x軸的平行線分別交雙曲線y= ![]() (x>0)和y=﹣
(x>0)和y=﹣ ![]() (x<0)于點M、N.
(x<0)于點M、N. 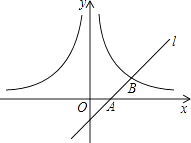
(1)求m的值和直線l的解析式;
(2)若點P在直線y=2上,求證:△PMB∽△PNA;
(3)是否存在實數p,使得S△AMN=4S△AMP?若存在,請求出所有滿足條件的p的值;若不存在,請說明理由.
【答案】
(1)解:∵B(2,1)在雙曲線y= ![]() (x>0)上,
(x>0)上,
∴m=2,
設直線l的解析式為y=kx+b,
則 ![]() ,
,
解得 ![]() ,
,
∴直線l的解析式為y=x﹣1
(2)證明:∵點P(p,p﹣1)(p>1),點P在直線y=2上,
∴p﹣1=2,
解得p=3,
∴P(3,2),
∴PM=2,PN=4,PA=2 ![]() ,PB=
,PB= ![]() ,
,
∵∠BPM=∠APN,PM:PN=PB:PA=1:2,
∴△PMB∽△PNA
(3)解:存在實數p,使得S△AMN=4S△AMP.
∵P(p,p﹣1)(p>1),
∴點M、N的縱坐標都為p﹣1,
將y=p﹣1代入y= ![]() 和y=﹣
和y=﹣ ![]() ,
,
得x= ![]() 和x=﹣
和x=﹣ ![]() ,
,
∴M、N的坐標分別為( ![]() ,p﹣1),(﹣
,p﹣1),(﹣ ![]() ,p﹣1),
,p﹣1),
①當1<p<2時,
MN= ![]() ,PM=
,PM= ![]() ﹣p,
﹣p,
∵S△AMN= ![]() MN×(p﹣1)=2,S△AMP=
MN×(p﹣1)=2,S△AMP= ![]() MP×(p﹣1)=﹣
MP×(p﹣1)=﹣ ![]() p2+
p2+ ![]() p+1,
p+1,
S△AMN=4S△AMP,
∴2=4×(﹣ ![]() p2+
p2+ ![]() p+1),
p+1),
整理,得p2﹣p﹣1=0,
解得:p= ![]() ,
,
∵1<p<2,
∴p= ![]() ,
,
②當p>2時,
MN= ![]() ,PM=p﹣
,PM=p﹣ ![]() ,
,
∵S△AMN= ![]() MN×(p﹣1)=2,S△AMP=
MN×(p﹣1)=2,S△AMP= ![]() MP×(p﹣1)=
MP×(p﹣1)= ![]() p2﹣
p2﹣ ![]() p﹣1,
p﹣1,
S△AMN=4S△AMP,
∴2=4×( ![]() p2﹣
p2﹣ ![]() p﹣1),
p﹣1),
整理,得p2﹣p﹣3=0,解得p= ![]() ,
,
∵p大于2,
∴p= ![]() ,
,
∴存在實數p= ![]() 或
或 ![]() 使得S△AMN=4S△AMP.
使得S△AMN=4S△AMP.

【解析】(1)將點B的坐標代入即可得出m的值,設直線l的解析式為y=kx+b,再把點A、B的坐標代入,解方程組求得k和b即可得出直線l的解析式;(2)根據點P在直線y=2上,求出點P的坐標,再證明△PMB∽△PNA即可;(3)先假設存在,利用S△AMN=4S△AMP . 求得p的值,看是否符合要求.
【考點精析】本題主要考查了確定一次函數的表達式和相似三角形的判定與性質的相關知識點,需要掌握確定一個一次函數,需要確定一次函數定義式y=kx+b(k不等于0)中的常數k和b.解這類問題的一般方法是待定系數法;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】已知二次函數y=﹣ ![]() x2﹣x+
x2﹣x+ ![]() .
. 
(1)在給定的直角坐標系中,畫出這個函數的圖象;
(2)根據圖象,寫出當y<0時,x的取值范圍;
(3)若將此圖象沿x軸向右平移3個單位,請寫出平移后圖象所對應的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面內4條直線l1、l2、l3、l4是一組平行線,相鄰2條平行線的距離都是1個單位長度,正方形ABCD的4個頂點A、B、C、D都在這些平行線上,其中點A、C分別在直線l1、l4上,該正方形的面積是平方單位. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠A=36°,AB=AC,AB的垂直平分線OD交AB于點O,交AC于點D,連接BD.下列結論錯誤的是( )

A. ∠C=2∠A B. BD平分∠ABC C. S△BCD=S△BOD D. 點D為線段AC的黃金分割點
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,三個半圓依次相外切,它們的圓心都在x軸上,并與直線y= ![]() x相切.設三個半圓的半徑依次為r1、r2、r3 , 則當r1=1時,r3= .
x相切.設三個半圓的半徑依次為r1、r2、r3 , 則當r1=1時,r3= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在社區全民健身活動中,父子倆參加跳繩比賽.相同時間內父親跳180個,兒子跳210個.已知兒子每分鐘比父親多跳20個,父親、兒子每分鐘各跳多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從3名男生和2名女生中隨機抽取2014年南京青奧會志愿者.求下列事件的概率:
(1)抽取1名,恰好是女生;
(2)抽取2名,恰好是1名男生和1名女生.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,E在BA的延長線上,AD平分∠CAE. 
(1)求證:AD∥BC;
(2)過點C作CG⊥AD于點F,交AE于點G,若AF=4,求BC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com