
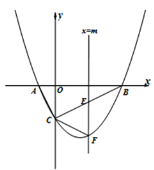
【題目】如圖,拋物線![]() 與x軸交于A、B兩點,與y軸交于點C,已知A(–1,0),且直線BC的解析式為y=
與x軸交于A、B兩點,與y軸交于點C,已知A(–1,0),且直線BC的解析式為y=![]() x-2,作垂直于x軸的直線
x-2,作垂直于x軸的直線![]() ,與拋物線交于點F,與線段BC交于點E(不與點B和點C重合).
,與拋物線交于點F,與線段BC交于點E(不與點B和點C重合).
(1)求拋物線的解析式;
(2)若△CEF是以CE為腰的等腰三角形,求m的值;
(3)點P為y軸左側拋物線上的一點,過點P作![]() 交直線BC于點M,連接PB,若以P、M、B為頂點的三角形與△ABC相似,求P點的坐標.
交直線BC于點M,連接PB,若以P、M、B為頂點的三角形與△ABC相似,求P點的坐標.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)符合條件的點P為P1(-1,0)或
;(3)符合條件的點P為P1(-1,0)或![]()
【解析】
(1)將y=0代入y=![]() x-2中,即可求出點B的坐標,然后利用待定系數法即可求出拋物線的解析式;
x-2中,即可求出點B的坐標,然后利用待定系數法即可求出拋物線的解析式;
(2)先分別用m表示出點E和點F的坐標,然后根據勾股定理分別求出CE2、CF2和EF2,然后根據等腰三角形腰的情況分類討論,分別求出對應的m值即可;
(3)根據勾股定理的逆定理證出△ABC為直角三角形,∠ACB=90°,然后根據相似三角形的對應情況分類討論,利用相似三角形的判定及性質和銳角三角函數即可求出結論.
解:(1) 由題意得:![]()
將y=0代入y=![]() x-2中,得x=4
x-2中,得x=4
∴點B的坐標為(4,0)
將A(-1,0),B(4,0)代入![]() 得
得
![]() ,
,
解得,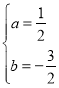
![]()
(2) ![]()
∴![]()
![]()
![]()
(i) 若以C為等腰三角形的頂點,則CE2=CF2
∴![]()
解得:m1=2,m2=4(不符合前提條件,故舍去);
(ii) 若以E為等腰三角形的頂點,則EC2=EF2
∴![]()
解得:![]() (不符合前提條件,故舍去);
(不符合前提條件,故舍去);
綜上:m=2或![]()
(3) ①根據勾股定理可得:AC=![]() =
=![]() ,BC=
,BC=![]() =
=![]() ,AB=5
,AB=5
∴AC2+BC2=25=AB2,
∴△ABC為直角三角形,∠ACB=90°
∴當點P與點A重合時,點M與點C重合,此時P1(-1,0),
②如圖,當△BPM∽△ABC時,
∴∠BPM=∠ABC
過點M作HR∥x軸,作PH⊥HR于點H,BR⊥HR與點R,
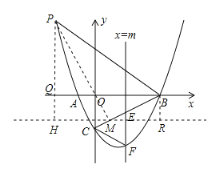
∴∠PHM=∠MRB=∠PMB=90°
∴∠HPM+∠PMH=90°,∠RMB+∠PMH=90°
∴∠HPM=∠RMB
∴△PHM∽△MRB
∴![]()
又∵AB//HR
∴![]()
∴![]()
令BR=a,MR=2a
又∵![]()
∴![]()
∴![]()
∴PH=4a,HM=2a,PQ=3a,
![]()
又∵點P在拋物線上,將![]() 代入
代入![]()
![]()
整理,得![]()
解得:![]() (舍),
(舍),![]()
∴![]()
∴符合條件的點P為P1(-1,0)或![]()


科目:初中數學 來源: 題型:
【題目】甲、乙兩人在一條長為600m的筆直道路上均勻地跑步,速度分別為![]() 和
和![]() ,起跑前乙在起點,甲在乙前面50m處,若兩人同時起跑,則從起跑出發到其中一人先到達終點的過程中,兩人之間的距離y(m)與時間t(s)的函數圖象是( )
,起跑前乙在起點,甲在乙前面50m處,若兩人同時起跑,則從起跑出發到其中一人先到達終點的過程中,兩人之間的距離y(m)與時間t(s)的函數圖象是( )
A.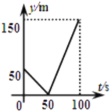 B.
B.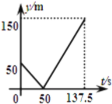 C.
C.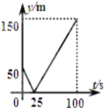 D.
D.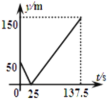
查看答案和解析>>
科目:初中數學 來源: 題型:
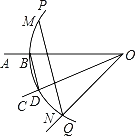
【題目】如圖:已知銳角∠AOC,依次按照以下順序操作畫圖:
(1)在射線OA上取一點B,以點O為圓心,OB長為半徑作![]() ,交射線OC于點D,連接BD;
,交射線OC于點D,連接BD;
(2)分別以點B,D為圓心,BD長為半徑作弧,交![]() 于點M,N;
于點M,N;
(3)連接ON,MN.
根據以上作圖過程及所作圖形可知下列結論:①OC平分∠AON;②MN∥BD;③MN=3BD;④若∠AOC=30°,則MN=![]() ON.其中正確結論的序號是_____.
ON.其中正確結論的序號是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
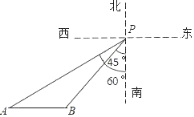
【題目】在某海域,一艘海監船在P處檢測到南偏西45°方向的B處有一艘不明船只,正沿正西方向航行,海監船立即沿南偏西60°方向以40海里/小時的速度去截獲不明船只,經過1.5小時,剛好在A處截獲不明船只,求不明船只的航行速度.(![]() ≈1.41,
≈1.41,![]() ≈1.73,結果保留一位小數).
≈1.73,結果保留一位小數).
查看答案和解析>>
科目:初中數學 來源: 題型:
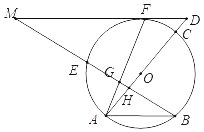
【題目】如圖,F為⊙O上的一點,過點F作⊙O的切線與直徑AC的延長線交于點D,過圓上的另一點B作AO的垂線,交DF的延長線于點M,交⊙O于點E,垂足為H,連接AF,交BM于點G.
(1)求證:△MFG為等腰三角形.
(2)若AB∥MD,求MF、FG、EG之間的數量關系,并說明理由.
(3)在(2)的條件下,若DF=6,tan∠M=![]() ,求AG的長.
,求AG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
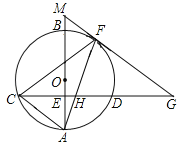
【題目】如圖,AB是⊙O的直徑,CD⊥AB,交⊙O于C、D兩點,交AB點E、F是弧BD上一點,過點F作一條直線,交CD的延長線于點G,交AB的延長線于點M.連結AF,交CD于點H,GF=GH.
(1)求證:MG是⊙O的切線;
(2)若弧AF=弧CF,求證:HC=AC;
(3)在(2)的條件下,若tanG=![]() ,AE=6,求GM的值.
,AE=6,求GM的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O是△ABC的外接圓,AE平分∠BAC交⊙O于點E,交BC于點D,過點E做直線l∥BC.
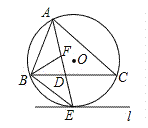
(1)判斷直線l與⊙O的位置關系,并說明理由;
(2)若∠ABC的平分線BF交AD于點F,求證:BE=EF;
(3)在(2)的條件下,若DE=4,DF=3,求AF的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com