
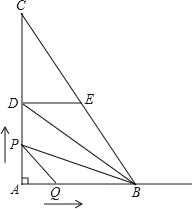
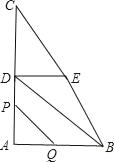
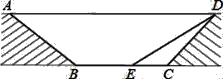
【題目】如圖,在直角△ABC中,∠A=90°,AB=6,AC=8.D、E分別是AC、BC邊的中點,點P從A出發沿線段AD﹣DE﹣EB以每秒3個單位長的速度向B勻速運動;點Q從點A出發沿射線AB以每秒2個單位長的速度勻速運動,當點P與點B重合時停止運動,點Q也隨之停止運動,設點P、Q運動時間是t秒,(t>0)
(1)當t= 時,點P到達終點B;
(2)當點P運動到點D時,求△BPQ的面積;
(3)設△BPQ的面積為S,求出點Q在線段AB上運動時,S與t的函數關系式;
(4)請直接寫出PQ∥DB時t的值.
【答案】(1)4秒;(2)![]() ;(3)Q在線段AB上運動時,S與t的函數關系式為S=
;(3)Q在線段AB上運動時,S與t的函數關系式為S=![]() ,(4)
,(4)![]()
【解析】
(1)由已知和勾股定理先求出BC,再由D,E分別是AC,BC的中點,求出AD、DE、BE,從而求出t;
(2)先求出當點P運動到點D時所用時間,得出AQ的長,即可求出BQ的長,再根據△BPQ的面積=![]() BQAP進行計算即可;
BQAP進行計算即可;
(3)由已知用t表示出AQ、AP、BQ,再由∠A=90°,通過面積公式求出S與t的函數關系式;
(4)通過假設,分兩種情況討論即可求解.
(1)已知Rt△ABC中,∠A=90°,AB=6,AC=8,
由勾股定理得:BC=![]() =
=![]() =10,
=10,
又由D,E分別是AC,BC的中點,
∴AD=4,DE=3,BE=5,
∴當點P到達終點B時所用時間t=(4+3+5)÷3=4(秒),
答t的值為4秒.
(2)當點P運動到點D時,所用時間為![]() 秒,
秒,
所以AQ=![]() ×2=
×2=![]() ,
,
∴BQ=6﹣![]() =
=![]() ,
,
∴△BPQ的面積=![]() BQAP=
BQAP=![]() ×4=
×4=![]() ;
;
(3)①如圖,當點P在AD上(不包含D點),
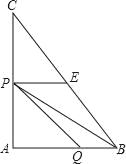
由已知得:AQ=2t,AP=3t,
∴BQ=AB﹣AQ=6﹣2t,
已知∠A=90°,
∴△BPQ的面積S=![]() BQAP=
BQAP=![]() (6﹣2t)3t=﹣3t2+9t,
(6﹣2t)3t=﹣3t2+9t,
所以Q在線段AB上運動時,S與t的函數關系式為S=﹣3t2+9t;
②如圖當點P在DE(包括點D、E)上,
過點P作PF⊥AB于F,
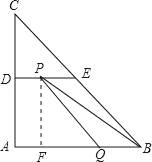
則PF=AD=4,
∴△BPQ的面積S=![]() BQPF=
BQPF=![]() (6﹣2t)4=12﹣4t,
(6﹣2t)4=12﹣4t,
所以此時Q在線段AB上運動時,S與t的函數關系式為S=12﹣4t;
③當點P在BE上(不包括E點),
由已知得:BP=3+4+5﹣3t=12﹣3t,
過點P作PF⊥AB于F,
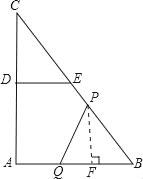
∴PF∥AC,
∴△BPF∽△BCA,
∴![]() ,
,
∴![]() ,
,
∴PF=![]() ,
,
∴△BPQ的面積S=![]() BQPF=
BQPF=![]() (6﹣2t)
(6﹣2t)![]() =
=![]() ,,
,,
所以Q在線段AB上運動時,S與t的函數關系式為S=![]() ,,
,,
(4)若PQ∥DB,則點P、Q必在DB同側.分兩種情況:
①當點Q在AB上,點P在AD上時,
假設PQ∥DB成立,
則△AQP∽△ABD,
∴![]() ,
,
∴![]() ,
,
此時方程的解是t=0,但此解不符合題意,
則PQ∥DB不成立,
②當3<t<4時,點Q在AB延長線上,點P在EB上,

此時PB=12﹣3t,PE=3t﹣7,BQ=2t﹣6.
若PQ∥DB,設直線PQ交DE與N,
∵DE∥AB,
∴△PEN∽△PBQ,
∴EN:BQ=PE:PB,
則EN=![]() ;
;
又∵NQ∥DB,
∴EN:ED=EP:EB,
則EN=![]() ,
,
所以![]() =
=![]() ,
,
解得t=![]() 符合題意.
符合題意.
綜上所述,當t=![]() 時,PQ∥DB.
時,PQ∥DB.


科目:初中數學 來源: 題型:
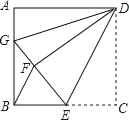
【題目】如圖,正方形ABCD中,AB=12,點E在邊BC上,BE=EC,將△DCE沿DE對折至△DFE,延長EF交邊AB于點G,連接DG、BF,給出下列結論:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=![]() .其中正確結論的個數是( )
.其中正確結論的個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
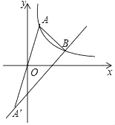
【題目】平面直角坐標系xOy中,橫坐標為a的點A在反比例函數y1=![]() (x>0)的圖象上.點A與點A關于點O對稱,一次函數y2=mx+n的圖象經過點A.
(x>0)的圖象上.點A與點A關于點O對稱,一次函數y2=mx+n的圖象經過點A.
(1)設a=2,點B(4,2)在函數y1,y2的圖象上.
①分別求函數y1,y2的表達式;
②直接寫出使y1>y2>0成立的x的范圍.
(2)如圖,設函數y1,y2的圖象相交于點B,點B的橫坐標為3a,△AA′B的面積為16,求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)一塊材料的形狀是銳角三角形ABC,邊BC=120mm,高AD=80mm,把它加工成正方形零件如圖1,使正方形的一邊在BC上,其余兩個頂點分別在AB、AC上.

(1)求證:△AEF∽△ABC;
(2)求這個正方形零件的邊長;
(3)如果把它加工成矩形零件如圖2,問這個矩形的最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在△ABC中,∠ABC=90°,AB=3,BC=4.點Q是線段AC上的一個動點,過點Q作AC的垂線交線段AB(如圖1)或線段AB的延長線(如圖2)于點P.
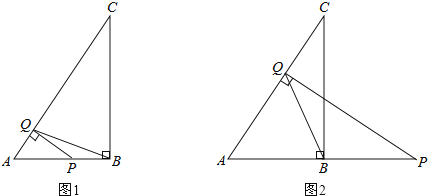
(1)當點P在線段AB上時,求證:△APQ∽△ABC;
(2)當△PQB為等腰三角形時,求AP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】舉世矚目的港珠澳大橋已于2018年10月24日正式通車,這座大橋是世界上最長的跨海大橋,被英國《衛報》譽為“新世界七大奇跡”,車輛經過這座大橋收費站時,從已開放的4個收費通道A、B、C、D中可隨機選擇其中一個通過.
(1)一輛車經過收費站時,選擇A通道通過的概率是 .
(2)用樹狀圖或列表法求兩輛車經過此收費站時,選擇不同通道通過的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為緩解交通擁堵,某區擬計劃修建一地下通道,該通道一部分的截面如圖所示(圖中地面AD與通道BC平行,通道水平寬度BC為8米,∠BCD=135°,通道斜面CD的長為6米,通道斜面AB的坡度i=1:![]() .
.
(1)求通道斜面AB的長;
(2)為增加市民行走的舒適度,擬將設計圖中的通道斜面CD的坡度變緩,修改后的通道斜面DE的坡角為30°,求此時BE的長.
(答案均精確到0.1米,參考數據:![]() ≈1.41,
≈1.41,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com