
【題目】如圖,在![]() 網(wǎng)格中,每個小正方形的邊長都為
網(wǎng)格中,每個小正方形的邊長都為![]() .
.
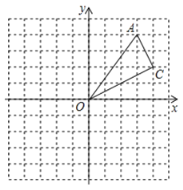
(1)建立如圖所示的平面直角坐標(biāo)系,若點![]() ,則點
,則點![]() 的坐標(biāo)_______________;
的坐標(biāo)_______________;
(2)將![]() 向左平移
向左平移![]() 個單位,向上平移
個單位,向上平移![]() 個單位,則點
個單位,則點![]() 的坐標(biāo)變?yōu)?/span>_____________;
的坐標(biāo)變?yōu)?/span>_____________;
(3)若將![]() 的三個頂點的橫縱坐標(biāo)都乘以
的三個頂點的橫縱坐標(biāo)都乘以![]() ,請畫出
,請畫出![]() ;
;
(4)圖中格點![]() 的面積是_________________;
的面積是_________________;
(5)在![]() 軸上找一點
軸上找一點![]() ,使得
,使得![]() 最小,請畫出點
最小,請畫出點![]() 的位置,并直接寫出
的位置,并直接寫出![]() 的最小值是______________.
的最小值是______________.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析;(4)5;(5)
;(3)見解析;(4)5;(5)![]()
【解析】
(1)根據(jù)第一象限點的坐標(biāo)特征寫出C點坐標(biāo);
(2)利用點平移的坐標(biāo)變換規(guī)律求解;
(3)將△AOC的三個頂點的橫縱坐標(biāo)都乘以- ![]() 得到A1、C1的坐標(biāo),然后描點即可;
得到A1、C1的坐標(biāo),然后描點即可;
(4)用一個矩形的面積分別減去三個三角形的面積去計算△AOC的面積;
(5)作C點關(guān)于x軸的對稱點C′,然后計算AC′即可.
解:(1)如圖,點![]() 的坐標(biāo)
的坐標(biāo)![]() ;
;
(2)將![]() 向左平移
向左平移![]() 個單位,向上平移
個單位,向上平移![]() 個單位,則點
個單位,則點![]() 的坐標(biāo)變?yōu)?/span>
的坐標(biāo)變?yōu)?/span>![]() ;
;
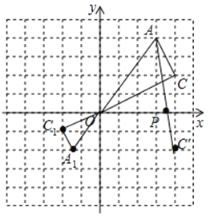
(3)如圖,![]() 為所作;
為所作;
(4)圖中格點![]() 的面積
的面積![]() ;
;
(5)如圖,作C關(guān)于x軸的對待點C’,連接C’A交x軸于點P,點![]() 即為所求作的點,
即為所求作的點,
![]() 的最小值
的最小值![]() .
.
故答案為(1)![]() ;(2)
;(2)![]() ;(4)
;(4)![]() ;(5)
;(5)![]() .
.


 新思維假期作業(yè)暑假吉林大學(xué)出版社系列答案
新思維假期作業(yè)暑假吉林大學(xué)出版社系列答案 藍(lán)天教育暑假優(yōu)化學(xué)習(xí)系列答案
藍(lán)天教育暑假優(yōu)化學(xué)習(xí)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
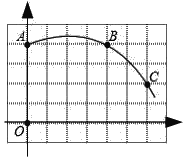
【題目】如圖,網(wǎng)格紙中每個小正方形的邊長為1,一段圓弧經(jīng)過格點,點O為坐標(biāo)原點.
(1)該圖中弧所在圓的圓心D的坐標(biāo)為 ;.
(2)根據(jù)(1)中的條件填空:
①圓D的半徑= (結(jié)果保留根號);
②點(7,0)在圓D (填“上”、“內(nèi)”或“外”);
③∠ADC的度數(shù)為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,直線![]() 分別與
分別與![]() 軸交于
軸交于![]() 兩點,過點
兩點,過點![]() 的直線交
的直線交![]() 軸負(fù)半軸于
軸負(fù)半軸于![]() ,且
,且![]() .
.

(1)求直線![]() 的函數(shù)表達(dá)式:
的函數(shù)表達(dá)式:
(2)如圖2, ![]() 為
為![]() 軸上
軸上![]() 點右側(cè)的一動點,以
點右側(cè)的一動點,以![]() 為直角頂點,
為直角頂點,![]() 為一腰在第一象限內(nèi)作等腰直角三角形
為一腰在第一象限內(nèi)作等腰直角三角形![]() ,連接
,連接![]() 并延長交
并延長交![]() 軸于點
軸于點![]() .當(dāng)
.當(dāng)![]() 點運(yùn)動時,
點運(yùn)動時,![]() 點的位置是否發(fā)生變化?如果不變請求出它的坐標(biāo):如果變化,請說明理由.
點的位置是否發(fā)生變化?如果不變請求出它的坐標(biāo):如果變化,請說明理由.
(3)直線![]() 交
交![]() 于
于![]() ,交
,交![]() 于點
于點![]() ,交
,交![]() 軸于
軸于![]() ,是否存在這樣的直線
,是否存在這樣的直線![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
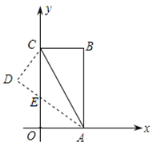
【題目】如圖,把長方形紙片![]() 放入平面直角坐標(biāo)系中,使
放入平面直角坐標(biāo)系中,使![]() ,
,![]() 分別落在
分別落在![]() 軸、
軸、![]() 軸上,連接
軸上,連接![]() ,將紙片
,將紙片![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 落在點
落在點![]() 的位置,
的位置,![]() 與
與![]() 軸交于點
軸交于點![]() ,若
,若![]() ,則
,則![]() 的長為( )
的長為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】由于受到手機(jī)更新?lián)Q代的影響,某手機(jī)店經(jīng)銷的華為![]() 手機(jī)四月售價比三月每臺降價
手機(jī)四月售價比三月每臺降價![]() 元.如果賣出相同數(shù)量的華為
元.如果賣出相同數(shù)量的華為![]() 手機(jī),那么三月銷售額為
手機(jī),那么三月銷售額為![]() 元,四月銷售額只有
元,四月銷售額只有![]() 元.
元.
(1)填表:
銷售額(元) | 單價(元 | 銷售手機(jī)的數(shù)量(臺) | |
三月 |
|
| ___________ |
四月 |
| __________ | ___________ |
(2)三、四月華為![]() 手機(jī)每臺售價各為多少元?
手機(jī)每臺售價各為多少元?
(3)為了提高利潤,該店計劃五月購進(jìn)華為![]() 手機(jī)銷售,已知華為
手機(jī)銷售,已知華為![]() 每臺進(jìn)價為
每臺進(jìn)價為![]() 元,華為
元,華為![]() 每臺進(jìn)價為
每臺進(jìn)價為![]() 元,調(diào)進(jìn)一部分資金購進(jìn)這兩種手機(jī)共
元,調(diào)進(jìn)一部分資金購進(jìn)這兩種手機(jī)共![]() 臺(其中華為
臺(其中華為![]() 有
有![]() 臺),在銷售中決定在四月售價基礎(chǔ)上每售出一臺華為
臺),在銷售中決定在四月售價基礎(chǔ)上每售出一臺華為![]() 手機(jī)再返還顧客現(xiàn)金
手機(jī)再返還顧客現(xiàn)金![]() 元,而華為
元,而華為![]() 按銷售價
按銷售價![]() 元銷售,若將這
元銷售,若將這![]() 臺手機(jī)全部售出共獲得多少利潤?
臺手機(jī)全部售出共獲得多少利潤?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
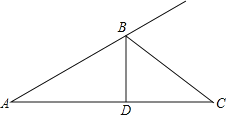
【題目】如圖,在△ABC中,BD⊥AC,垂足為C,且∠A<∠C,點E是一動點,其在BC上移動,連接DE,并過點E作EF⊥DE,點F在AB的延長線上,連接DF交BC于點G.
(1)請同學(xué)們根據(jù)以上提示,在上圖基礎(chǔ)上補(bǔ)全示意圖.
(2)當(dāng)△ABD與△FDE全等,且AD=FE,∠A=30°,∠AFD=40°,求∠C的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
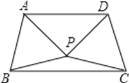
【題目】如圖,△ABP與![]() 是兩個全等的等邊三角形,且
是兩個全等的等邊三角形,且![]() ,有下列四個結(jié)論:①
,有下列四個結(jié)論:①![]() ,②
,②![]() ,③
,③![]() ,④四邊形ABCD是軸對稱圖形,其中正確的有
,④四邊形ABCD是軸對稱圖形,其中正確的有
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com