【題目】如圖，在正方形
中，點
的坐標是
，則
點的坐標是( )
A.
B.
C.
D.
【答案】A
【解析】
作CD⊥x軸于D，作AE⊥x軸于E，由AAS證明△AOE≌△OCD，得出AE=OD，OE=CD，由點A的坐標是（-3，1），得出OE=3，AE=1，∴OD=1，CD=3，得出C（1，3）即可．
解：如圖所示：作CD⊥x軸于D，作AE⊥x軸于E，
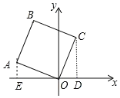
則∠AEO=∠ODC =90°，
∴∠OAE+∠AOE=90°，
∵四邊形OABC是正方形，
∴OA=CO，∠AOC=90°，
∴∠AOE+∠COD=90°，
∴∠OAE=∠COD，
在△AOE和△OCD中，
，
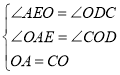∴△AOE≌△OCD（AAS），
∴AE=OD，OE=CD，
∵點A的坐標是（-3，1），
∴OE=3，AE=1，
∴OD=1，CD=3，
∴C（1，3），故選：A．
中考解讀考點精練系列答案科目：初中數學 來源： 題型：
【題目】某市政府大力扶持大學生創業．李明在政府的扶持下投資銷售一種進價為每件20元的護眼臺燈．銷售過程中發現，每月銷售量y（件）與銷售單價x（元）之間的關系可近似的看作一次函數： 
．
（1）設李明每月獲得利潤為w（元），當銷售單價定為多少元時，每月可獲得最大利潤？
（2）如果李明想要每月獲得2000元的利潤，那么銷售單價應定為多少元？
（3）根據物價部門規定，這種護眼臺燈的銷售單價不得高于32元，如果李明想要每月獲得的利潤不低于2000元，那么他每月的成本最少需要多少元？（成本＝進價×銷售量）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如果二次函數的二次項系數為1，那么此二次函數可表示為y＝x2＋px＋q，我們稱[p，q]為此函數的特征數，如函數y＝x2＋2x＋3的特征數是[2，3]．
(1)若一個函數的特征數為[－2，1]，求此函數圖象的頂點坐標；
(2)探究下列問題：
①若一個函數的特征數為[4，－1]，將此函數的圖象先向右平移1個單位長度，再向上平移1個單位長度，求得到的圖象對應的函數的特征數；
②若一個函數的特征數為[2，3]，問此函數的圖象經過怎樣的平移，才能使得到的圖象對應的函數的特征數為[3，4]?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線y＝(m－1)x2＋m2－2m－2的圖象開口向下，且經過點(0，1)．
(1)求m的值；
(2)求此拋物線的頂點坐標及對稱軸；
(3)當x為何值時，y隨x的增大而增大？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市居民用電的電價實行階梯收費，收費標準如下表：
一戶居民每月用電量x（單位：度） | 電費價格（單位：元/度） |
0＜x≤200 | a |
200＜x≤400 | b |
x＞400 | 0.92 |
（1）已知李叔家四月份用電286度，繳納電費178.76元；五月份用電316度，繳納電費198.56元，請你根據以上數據，求出表格中a，b的值．
（2）六月份是用電高峰期，李叔計劃六月份電費支出不超過300元，那么李叔家六月份最多可用電多少度？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△BAD是由△BEC在平面內繞點B旋轉60°而得，且AB⊥BC，BE＝CE，連接DE.
（1）求證：△BDE≌△BCE；
（2）試判斷四邊形ABED的形狀，并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
