
【題目】已知:如圖,平行四邊形ABCD的對角線相交于點O,點E在邊BC的延長線上,且OE=OB,聯結DE.
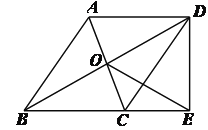
(1)求證:DE⊥BE;
(2)如果OE⊥CD,求證:BD ![]() CE=CD
CE=CD ![]() DE.
DE.
【答案】(1)證明見解析;(2)證明見解析.
【解析】
試題分析:(1)由平行四邊形的性質得到BO=![]() BD,由等量代換推出OE=
BD,由等量代換推出OE=![]() BD,根據平行四邊形的判定即可得到結論;
BD,根據平行四邊形的判定即可得到結論;
(2)根據等角的余角相等,得到∠CEO=∠CDE,推出△BDE∽△CDE,即可得到結論.
試題解析:(1)∵四邊形ABCD是平行四邊形,
∴BO=OD,
∵OE=OB,
∴OE=OD,
∴∠OBE=∠OEB,∠OED=∠ODE,
∵∠OBE+∠OEB+∠OED+∠ODE=180°,
∴∠BEO+∠DEO=∠BED=90°,
∴DE⊥BE;
(2)∵OE⊥CD
∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵OB=OE,
∴∠DBE=∠CDE,
∵∠BED=∠BED,
∴△BDE∽△DCE,
∴![]() ,
,
∴BD ![]() CE=CD
CE=CD ![]() DE.
DE.


科目:初中數學 來源: 題型:
【題目】如圖,AB、CD為兩個建筑物,建筑物AB的高度為60m,從建筑物AB的頂部A點測得建筑物CD的頂部C點的俯角∠EAC為30°,測得建筑物CD的底部D點的俯角∠EAD為45°.
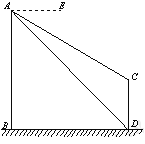
(1)求兩建筑物兩底部之間的水平距離BD的長度;
(2)求建筑物CD的高度(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ ABC中,∠ ABC、∠ ACB的平分線交于點O。
(1)若∠ABC=40°,∠ ACB=50°,則∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°,則∠BOC=________
(3)若∠A=70°,則∠BOC=_________
(4)若∠BOC=140°,則∠A=________
(5)你能發現∠ BOC與∠ A之間有什么數量關系嗎?寫出并說明理由。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查方式的選取不恰當的是( )
A. 為了解初一(2)班全班同學每周體育鍛煉的時間,采取普查的方式
B. 為了解某個十字路口的車流量,采取抽樣調查的方式
C. 為了解人們保護水資源的意識,采取抽樣調查的方式
D. 對“嫦娥三號”衛星零部件的檢查,采取抽樣調查的方式
查看答案和解析>>
科目:初中數學 來源: 題型:
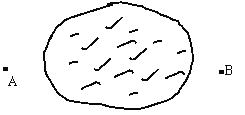
【題目】圖為人民公園中的荷花池,現要測量此荷花池兩旁A、B兩棵樹間的距離(我們不能直接量得).請你根據所學知識,以卷尺和測角儀為測量工具設計一種測量方案.
要求:(1)畫出你設計的測量平面圖;
(2)簡述測量方法,并寫出測量的數據(長度用![]() …表示;角度用
…表示;角度用![]() …表示);
…表示);
(3)根據你測量的數據,計算A、B兩棵樹間的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面的證明.
(1)如圖,AB∥CD,CB∥DE.求證:∠B+∠D=180°.

證明:∵AB∥CD,
∴∠B=( ① )( ② );
∵CB∥DE,
∴∠C+∠D=180°( ③ ).
∴∠B+∠D=180°.
(2)如圖,∠ABC=∠A′B′C′,BD,B′D′分別是∠ABC,∠A′B′C′的平分線.求證:∠1=∠2.

證明:∵BD, B′D′分別是∠ABC,∠A′B′C′的平分線,
∴∠1=![]() ∠ABC,∠2=( ④ )( ⑤ ).
∠ABC,∠2=( ④ )( ⑤ ).
又∠ABC=∠A′B′C′,
∴![]() ∠ABC=
∠ABC=![]() ∠A′B′C′.
∠A′B′C′.
∴∠1=∠2( ⑥ ).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com