【題目】如圖，在菱形ABCD中，∠ABC與∠BAD的度數比為1：2，周長是40cm．求：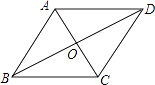 
（1）兩條對角線AC、BD的長度；
（2）菱形ABCD的面積．
【答案】
（1）解：∵四邊形ABCD是菱形，
∴AB=BC，AC⊥BD，AD∥BC，
∴∠ABC+∠BAD=180°，
∵∠ABC與∠BAD的度數比為1：2，
∴∠ABC= 
×180°=60°，
∴∠ABO= ∠ABC=30°，
∵菱形ABCD的周長是40cm．
∴AB=10cm，
∴OA= AB=5cm，
∴OB= 
=5 
，
∴AC=2OA=10cm，BD=2OB=10 cm
（2）解：S菱形ABCD= ACBD= ×10×10 =50 （cm2）
【解析】（1）由在菱形ABCD中，∠ABC與∠BAD的度數比為1：2，周長是40cm，可求得△ABO是含30°角的直角三角形，AB=10cm，繼而求得AC與BD的長；（2）由菱形的面積等于其對角線積的一半，即可求得答案．
【考點精析】通過靈活運用菱形的性質，掌握菱形的四條邊都相等；菱形的對角線互相垂直，并且每一條對角線平分一組對角；菱形被兩條對角線分成四個全等的直角三角形；菱形的面積等于兩條對角線長的積的一半即可以解答此題．
新課標快樂提優暑假作業陜西旅游出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案科目：初中數學 來源： 題型：
【題目】動物園中有熊貓、孔雀、大象、梅花鹿四種可愛的動物，為了解本班同學喜歡哪種動物的人最多，需要進行調查，則調查的對象是( )
A. 本班的每一名同學 B. 熊貓、孔雀、大象、梅花鹿
C. 同學們的選票 D. 記錄下來的數據
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=kx+b的圖象分別與反比例函數y=
的圖象在第一象限交于點A（4，3），與y軸的負半軸交于點B，且OA=OB．
（1）求函數y=kx+b和y=
的表達式；
（2）已知點C（0，5），試在該一次函數圖象上確定一點M，使得MB=MC，求此時點M的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校一課外活動小組為了解學生最喜歡的球類運動情況，隨機抽查本校九年級的200名學生，調查的結果如圖所示．請根據該扇形統計圖解答以下問題：
（1）求圖中的x的值；
（2）求最喜歡乒乓球運動的學生人數；
（3）若由3名最喜歡籃球運動的學生，1名最喜歡乒乓球運動的學生，1名最喜歡足球運動的學生組隊外出參加一次聯誼活動．欲從中選出2人擔任組長（不分正副），列出所有可能情況，并求2人均是最喜歡籃球運動的學生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】直角三角板ABC中，∠A=30°，BC＝1.將其繞直角頂點C逆時針旋轉一個角
（
且
），得到Rt△
.
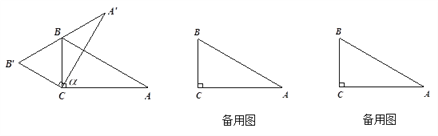
（1）如圖，當邊
經過點B時，求旋轉角的度數；
（2）在三角板旋轉的過程中，邊
與AB所在直線交于點D，過點 D作DE∥交
邊于點E，聯結BE.
①當
時，設AD=
，BE=
，求與之間的函數解析式及自變量 的取值范圍；
②當
時，求AD的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，一次函數y=kx+b（k≠0）的圖象與反比例函數
（m≠0）的圖象交于A、B兩點，與x軸交于C點，點A的坐標為（n，6），點C的坐標為（﹣2，0），且tan∠ACO=2．
（1）求該反比例函數和一次函數的解析式；
（2）求點B的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了增強環境保護意識，6月5日“世界環境日”當天，在環保局工作人員指導下，若干名“環保小衛士”組成的“控制噪聲污染”課題學習研究小組，抽樣調查了全市40個噪聲測量點在某時刻的噪聲聲級（單位：dB），將調查的數據進行處理（設所測數據是正整數），得不完整頻數分布表和頻數分布直方圖如下：
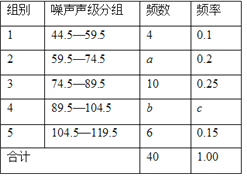
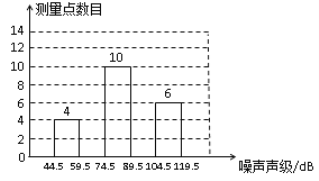
根據表中提供的信息解答下列問題：
（1）頻數分布表中的a =________，b=________，c =_________；
（2）請補全頻數分布直方圖；
（3）如果全市共有200個測量點，那么在這一時刻噪聲聲級小于75dB的測量點約有多少個？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com