
【題目】如圖,在平面直角坐標系中,一次函數y=kx+b(k≠0)的圖象與反比例函數![]() (m≠0)的圖象交于A、B兩點,與x軸交于C點,點A的坐標為(n,6),點C的坐標為(﹣2,0),且tan∠ACO=2.
(m≠0)的圖象交于A、B兩點,與x軸交于C點,點A的坐標為(n,6),點C的坐標為(﹣2,0),且tan∠ACO=2.
(1)求該反比例函數和一次函數的解析式;
(2)求點B的坐標.

【答案】(1)![]() ,y=2x+4;(2)B(﹣3,﹣2).
,y=2x+4;(2)B(﹣3,﹣2).
【解析】
試題分析:(1)先過點A作AD⊥x軸,根據tan∠ACO=2,求得點A的坐標,進而根據待定系數法計算兩個函數解析式;(2)先聯立兩個函數解析式,再通過解方程求得交點B的坐標即可.
試題解析:(1)過點A作AD⊥x軸,垂足為D.由A(n,6),C(﹣2,0)可得,OD=n,AD=6,CO=2
∵tan∠ACO=2,∴![]() =2,即
=2,即![]() ,∴n=1,∴A(1,6).將A(1,6)代入反比例函數,得m=1×6=6,∴反比例函數的解析式為
,∴n=1,∴A(1,6).將A(1,6)代入反比例函數,得m=1×6=6,∴反比例函數的解析式為![]() .
.
將A(1,6),C(﹣2,0)代入一次函數y=kx+b,可得:![]() ,解得:
,解得:![]() ,∴一次函數的解析式為y=2x+4;
,∴一次函數的解析式為y=2x+4;
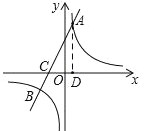
(2)由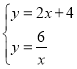 可得,
可得,![]() ,解得
,解得![]() =1,
=1,![]() =﹣3.∵當x=﹣3時,y=﹣2,∴點B坐標為(﹣3,﹣2).
=﹣3.∵當x=﹣3時,y=﹣2,∴點B坐標為(﹣3,﹣2).


科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠ABC與∠BAD的度數比為1:2,周長是40cm.求: 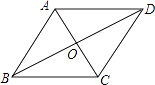
(1)兩條對角線AC、BD的長度;
(2)菱形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若拋物線L:y=ax2+bx+c(a,b,c是常數,abc≠0)與直線l都經過y軸上的一點P,且拋物線L的頂點Q在直線l上,則稱此直線l與該拋物線L具有“一帶一路”關系.此時,直線l叫做拋物線L的“帶線”,拋物線L叫做直線l的“路線”.
(1)若直線y=mx+1與拋物線y=x2﹣2x+n具有“一帶一路”關系,求m,n的值;
(2)若某“路線”L的頂點在反比例函數y=![]() 的圖象上,它的“帶線”l的解析式為y=2x﹣4,求此“路線”L的解析式;
的圖象上,它的“帶線”l的解析式為y=2x﹣4,求此“路線”L的解析式;
(3)當常數k滿足![]() ≤k≤2時,求拋物線L:y=ax2+(3k2﹣2k+1)x+k的“帶線”l與x軸,y軸所圍成的三角形面積的取值范圍.
≤k≤2時,求拋物線L:y=ax2+(3k2﹣2k+1)x+k的“帶線”l與x軸,y軸所圍成的三角形面積的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的布袋中裝有紅色、白色玻璃球共40個,除顏色外其他完全相同,小明通過多次摸球試驗后發現,其中摸到紅色球的頻率穩定在0.15左右,則口袋中紅色球可能有__________個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用配方法解一元二次方程x2﹣4x﹣5=0的過程中,配方正確的是( )
A. (x+2)2=1B. (x﹣2)2=1C. (x+2)2=9D. (x﹣2)2=9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成以下任務,適合用抽樣調查的是( )
A. 調查你班同學的年齡情況 B. 考察一批炮彈的殺傷半徑
C. 為訂購校服,了解學生衣服的尺寸 D. 對航天飛機上的零部件進行檢查
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com