
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() ,且滿足
,且滿足![]() .
.

(1)![]() 于
于![]() ,交
,交![]() 軸于
軸于![]() ,求
,求![]() 點坐標;
點坐標;
(2)過點![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的長;
的長;
(3)![]() 為第一象限一點,
為第一象限一點,![]() 交
交![]() 軸于
軸于![]() .在
.在![]() 上截取
上截取![]() ,
,![]() 為
為![]() 的中點,求
的中點,求![]() 的度數.
的度數.
【答案】(1)M(0,2);(2)AN=4;(3)∠OPF=45°.
【解析】
(1)先由條件推出△AOC是等腰直角三角形,再推出△BOM是等腰直角三角形,根據OB=2,得出OM=2,即可得出M的坐標;
(2)由等角的余角相等可得∠BCO=∠OAN=30°,再判定△BOC≌△NOA(ASA),得到BC=NA,再根據Rt△BOC中,BC=2BO=4,即可得AN=4;
(3)連接OF,把△OCF繞點O順時針旋轉90°至△OAD處,連接DP,由旋轉可得,AD=CF=EF,∠OCF=∠OAD,OF=OD,再判定△PEF≌△PAD,得出PF=PD,∠FPE=∠DPA,進而判定△OPF≌△OPD,即可出結果.
(1)由題可得,ac≥0,ca≥0,
∴a=c,即OA=OC,
∴△AOC是等腰直角三角形,
∴∠OAD=45,
又∵BD⊥AC,
∴∠ABD=45,
又∵∠BOM=90,
∴△BOM是等腰直角三角形,
∴OB=OM,
∵![]() ,且a=c,
,且a=c,
∴b=2,即OB=2,
∴OM=2,
∴M(0,2);
(2)∵∠CAN=15°,∠OAC=45°,
∴∠OAN=30°,
∵AG⊥BC,CO⊥AO,
∴∠CNG+∠BCO=90°,∠ANO+∠OAN=90°,
∵∠ANO=∠CNG,
∴∠BCO=∠OAN=30°,
在△BOC和△NOA中,
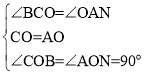
∴△BOC≌△NOA(ASA),
∴BC=NA,
又∵Rt△BOC中,∠BCO=30°,
∴BC=2BO=4,
∴AN=4;
(3)如圖3,連接OF,把△OCF繞點O順時針旋轉90°至△OAD處,連接DP,
由旋轉可得,AD=CF=EF,∠OCF=∠OAD,OF=OD,
∵∠AOQ+∠APQ=180°,
∴∠OAP+∠OQP=180°,
又∵∠EQC+∠OQP=180°,
∴∠OAP=∠EQC,
∴∠PEF=∠PAD,
在△PEF和△PAD中,
∴△PEF≌△PAD(SAS),
∴PF=PD,∠FPE=∠DPA,
∴∠FPD=∠QPA=90°,
∵在△OPF和△OPD中,
∴△OPF≌△OPD(SSS),
∴∠OPF=∠OPD=![]() ∠FPD=45°.
∠FPD=45°.


科目:初中數學 來源: 題型:
【題目】如圖,△ABP與![]() 是兩個全等的等邊三角形,且
是兩個全等的等邊三角形,且![]() ,有下列四個結論:①
,有下列四個結論:①![]() ,②
,②![]() ,③
,③![]() ,④四邊形ABCD是軸對稱圖形,其中正確的有
,④四邊形ABCD是軸對稱圖形,其中正確的有

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是
A.一個游戲中獎的概率是![]() ,則做100次這樣的游戲一定會中獎
,則做100次這樣的游戲一定會中獎
B.為了了解全國中學生的心理健康狀況,應采用普查的方式
C.一組數據0,1,2,1,1的眾數和中位數都是1
D.若甲組數據的方差![]() ,乙組數據的方差
,乙組數據的方差![]() ,則乙組數據比甲組數據穩定
,則乙組數據比甲組數據穩定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC與△DEC是兩個大小不同的等腰直角三角形.
(1)如圖①所示,連接AE,DB,試判斷線段AE和DB的數量和位置關系,并說明理由;
(2)如圖②所示,連接DB,將線段DB繞D點順時針旋轉90°到DF,連接AF,試判斷線段DE和AF的數量和位置關系,并說明理由.
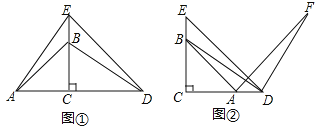
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰三角形ABC中,∠ABC=90度,D是AC邊上的動點,連結BD,E、F分別是AB、BC上的點,且DE⊥DF.、(1)如圖1,若D為AC邊上的中點.
(1)填空:∠C= ,∠DBC= ;
(2)求證:△BDE≌△CDF.
(3)如圖2,D從點C出發,點E在PD上,以每秒1個單位的速度向終點A運動,過點B作BP∥AC,且PB=AC=4,點E在PD上,設點D運動的時間為t秒(0≤1≤4)在點D運動的過程中,圖中能否出現全等三角形?若能,請直接寫出t的值以及所對應的全等三角形的對數,若不能,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】體育老師為了解本校九年級女生1分鐘“仰臥起坐”體育測試項目的達標情況,從該校九年級136名女生中,隨機抽取了20名女生,進行了1分鐘仰臥起坐測試,獲得數據如下:
收集數據:抽取20名女生的1分鐘仰臥起坐測試成績(個)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述數據:請你按如下分組整理、描述樣本數據,把下列表格補充完整:
范圍 | 25≤x≤29 | 30≤x≤34 | 35≤x≤39 | 40≤x≤44 | 45≤x≤49 | 50≤x≤54 | 55≤x≤59 |
人數 |
|
|
|
|
|
|
|
(說明:每分鐘仰臥起坐個數達到49個及以上時在中考體育測試中可以得到滿分)
(2)分析數據:樣本數據的平均數、中位數、滿分率如下表所示:
平均數 | 中位數 | 滿分率 |
46.8 | 47.5 | 45% |
得出結論:①估計該校九年級女生在中考體育測試中1分鐘“仰臥起坐”項目可以得到滿分的人數為 ;
②該中心所在區縣的九年級女生的1分鐘“仰臥起坐”總體測試成績如下:
平均數 | 中位數 | 滿分率 |
45.3 | 49 | 51.2% |
請你結合該校樣本測試成績和該區縣總體測試成績,為該校九年級女生的1分鐘“仰臥起坐”達標情況做一下評估,并提出相應建議.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某測量小組為了測量山BC的高度,在地面A處測得山頂B的仰角45°,然后沿著坡度為i=1:![]() 的坡面AD走了200米達到D處,此時在D處測得山頂B的仰角為60°,求山高BC(結果保留根號).
的坡面AD走了200米達到D處,此時在D處測得山頂B的仰角為60°,求山高BC(結果保留根號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() ,對角線
,對角線![]() ,
,![]() 相交于
相交于![]() 點,將直線
點,將直線![]() 繞點
繞點![]() 順時針旋轉,分別交
順時針旋轉,分別交![]() ,
,![]() 于點
于點![]() ,
,![]() ,下列說法不正確的是( )
,下列說法不正確的是( )

A. 當![]() 時,四邊形
時,四邊形![]() 一定為平行四邊形
一定為平行四邊形
B. 當四邊形![]() 為直角梯形時,線段
為直角梯形時,線段![]()
C. 當![]() 時,四邊形
時,四邊形![]() 一定為菱形
一定為菱形
D. 在旋轉的過程中,線段![]() 與
與![]() 總相等
總相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是某同學對多項式(x2-4x+2)(x2-4x+6)+4進行因式分解的過程.
解:設x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列問題:
(1)該同學第二步到第三步運用了因式分解的_______.
A.提取公因式 B.平方差公式 C.兩數和的完全平方公式 D.兩數差的完全平方公式
(2)該同學因式分解的結果是否徹底?________.(填“徹底”或“不徹底”)
若不徹底,請直接寫出因式分解的最后結果_________.
(3)請你模仿以上方法嘗試對多項式(x2-2x)(x2-2x+2)+1進行因式分解.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com