
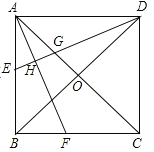
【題目】如圖,正方形ABCD中,O是對角線的交點,AF平分![]() BAC,DH
BAC,DH![]() AF于點H,交AC于G,DH延長線交AB于點E,求證:BE=2OG.
AF于點H,交AC于G,DH延長線交AB于點E,求證:BE=2OG.
 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線y=k1x(x≥0)與雙曲線y=![]() (x>0)相交于點P(2,4).已知點A(4,0),B(0,3),連接AB,將Rt△AOB沿OP方向平移,使點O移動到點P,得到△A′PB′.過點A′作A′C∥y軸交雙曲線于點C,連接CP.
(x>0)相交于點P(2,4).已知點A(4,0),B(0,3),連接AB,將Rt△AOB沿OP方向平移,使點O移動到點P,得到△A′PB′.過點A′作A′C∥y軸交雙曲線于點C,連接CP.
(1)求k1與k2的值;
(2)求直線PC的解析式;
(3)直接寫出線段AB掃過的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C在⊙O上,∠ABC的平分線與AC相交于點D,與⊙O過點A的切線相交于點E. 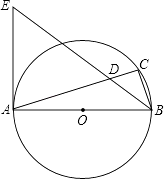
(1)∠ACB=°,理由是:;
(2)猜想△EAD的形狀,并證明你的猜想;
(3)若AB=8,AD=6,求BD.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,對角線AC、BD交于點O,E為OC上動點(與點O不重合),作AF⊥BE,垂足為G,交BO于H.連接OG、CG.
(1)求證:AH=BE;
(2)試探究:∠AGO 的度數是否為定值?請說明理由;
(3)若OG⊥CG,BG=![]() ,求△OGC的面積.
,求△OGC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,P為邊AB上一點.
(1)如圖1,若∠ACP=∠B,求證:AC2=APAB;
(2)若M為CP的中點,AC=2.
①如圖2,若∠PBM=∠ACP,AB=3,求BP的長;
②如圖3,若∠ABC=45°,∠A=∠BMP=60°,直接寫出BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》“勾股”章的問題::“今有二人同所立,甲行率七,乙行率三,乙東行,甲南行十步而斜東北與乙會.問甲、乙各行幾何?”大意是說:如圖,甲乙二人從A處同時出發,甲的速度與乙的速度之比為7:3,乙一直向東走,甲先向南走十步到達C處,后沿北偏東某方向走了一段距離后與乙在B處相遇,這時,甲乙各走了多遠?
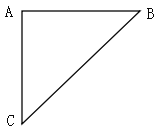
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上,點A表示﹣10,點B表示11,點C表示18.動點P從點A出發,沿數軸正方向以每秒2個單位的速度勻速運動;同時,動點Q從點C出發,沿數軸負方向以每秒1個單位的速度勻速運動.設運動時間為t秒.
(1)當t為何值時,P、Q兩點相遇?相遇點M所對應的數是多少?
(2)在點Q出發后到達點B之前,求t為何值時,點P到點O的距離與點Q到點B的距離相等;
(3)在點P向右運動的過程中,N是AP的中點,在點P到達點C之前,求2CN﹣PC的值.
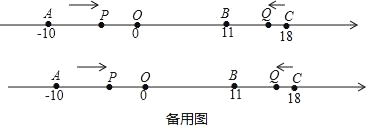
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一件工程甲獨做50天可完,乙獨做75天可完,現在兩個人合作,但是中途乙因事離開幾天,從開工后40天把這件工程做完,則乙中途離開了( )天.
A. 10 B. 20 C. 30 D. 25
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為減少環境污染,自2008年6月1日起,全國的商品零售場所開始實行“塑料購物袋有償使用制度”(以下簡稱“限塑令”).某班同學于6月上旬的一天,在某超市門口采用問卷調查的方式,隨機調查了“限塑令”實施前后,顧客在該超市用購物袋的情況,以下是根據100位顧客的100份有效答卷畫出的統計圖表的一部分: 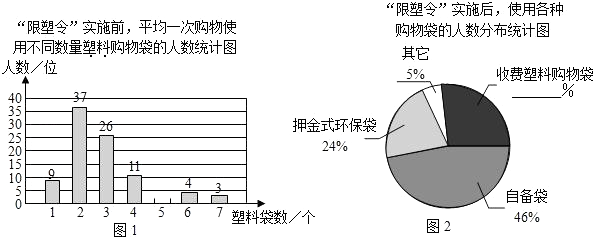
“限塑令”實施后,塑料購物袋使用后的處理方式統計表:
處理方式 | 直接丟棄 | 直接做垃圾袋 | 再次購物使用 | 其它 |
選該項的人數占 | 5% | 35% | 49% | 11% |
請你根據以上信息解答下列問題:
(1)補全圖1,“限塑令”實施前,如果每天約有2 000人次到該超市購物.根據這100位顧客平均一次購物使用塑料購物袋的平均數,估計這個超市每天需要為顧客提供多少個塑料購物袋?
(2)補全圖2,并根據統計圖和統計表說明,購物時怎樣選用購物袋,塑料購物袋使用后怎樣處理,能對環境保護帶來積極的影響.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com