
【題目】如圖,在![]() 內部做
內部做![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點:動點
的中點:動點![]() 由
由![]() 出發,沿
出發,沿![]() 運動,速度為每秒5個單位,動點
運動,速度為每秒5個單位,動點![]() 由
由![]() 出發,沿
出發,沿![]() 運動,速度為每秒8個單位,當點
運動,速度為每秒8個單位,當點![]() 到達點
到達點![]() 時,兩點同時停止運動;過
時,兩點同時停止運動;過![]() 、
、![]() 、
、![]() 作
作![]() ;
;
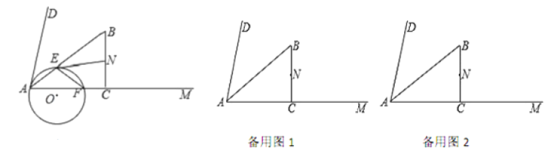
(1)判斷![]() 的形狀為________,并判斷
的形狀為________,并判斷![]() 與
與![]() 的位置關系為__________;
的位置關系為__________;
(2)求![]() 為何值時,
為何值時,![]() 與
與![]() 相切?求出此時
相切?求出此時![]() 的半徑,并比較半徑與劣弧
的半徑,并比較半徑與劣弧![]() 長度的大小;
長度的大小;
(3)直接寫出![]() 的內心運動的路徑長為__________;(注:當
的內心運動的路徑長為__________;(注:當![]() 、
、![]() 、
、![]() 重合時,內心就是
重合時,內心就是![]() 點)
點)
(4)直接寫出線段![]() 與
與![]() 有兩個公共點時,
有兩個公共點時,![]() 的取值范圍為__________.
的取值范圍為__________.
(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)△AEF為等腰三角形;DA與![]() 相切;(2)劣弧
相切;(2)劣弧![]() 長度>半徑;(3)
長度>半徑;(3)![]() 的內心運動的路徑長為
的內心運動的路徑長為![]() ;(4)線段
;(4)線段![]() 與
與![]() 有兩個公共點時,
有兩個公共點時,![]() 的取值范圍為
的取值范圍為![]() .
.
【解析】
(1)過點E作EH⊥AF于點H,連接OH,OA,證明△AEH∽△ABC,得到AH=FH,即可證明為等腰三角形;根據圓周角和圓心角證明∠DAC=∠AOE,即可證明∠DAO=90°;
(2)連接EO,AO,OF,交AC于點H,根據相切知四邊形EHCN為矩形,從而求出t,在Rt△AOH中,根據勾股定理求出半徑,然后求出∠AOH的度數即可比較;
(3)得到![]() 的內心運動的路徑長為AG,然后根據面積求出內切圓半徑,從而求出AG長;
的內心運動的路徑長為AG,然后根據面積求出內切圓半徑,從而求出AG長;
(4)分別討論兩種極限位置,①當MN與![]() 相切時,②當N在圓上時,即ON為半徑,分別求出t的值,即可確定t的取值范圍.
相切時,②當N在圓上時,即ON為半徑,分別求出t的值,即可確定t的取值范圍.
解:(1)過點E作EH⊥AF于點H,連接OH,OA,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
設運動時間為t,
∴AE=5t,AF=8t,
∵EH⊥AF,
∴△AEH∽△ABC,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴FH=4t,
∴AH=FH,
∴△AEF為等腰三角形;
∴E為![]() 的中點,
的中點,
∴H為AF的中點,
∴OH垂直AC,
∴∠OAF+∠AOE=90°,
∴∠AOE=2∠EFA,
∵AB平分∠DAC,∠EAC=∠EFA,
∴∠DAC=∠AOE,
∴∠DAC+∠AOE=90°,
∴∠DAO=90°,
∴DA與![]() 相切;
相切;
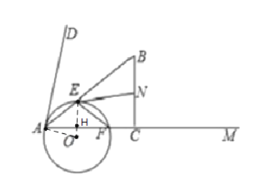
(2)連接EO,AO,OF,交AC于點H,
由(1)知EH⊥AC,
∵EN與![]() 相切,
相切,
∴∠OEN=90°,
∴四邊形EHCN為矩形,
在Rt△AHE中,
![]() ,
,
∴NC=EH=3t,
∵N是BC中點,
∴BC=6t,
∵BC=6,
∴6t=6,
解得:t=1,
∴AH=4,EH=3,
設半徑為x,
∴OH=x-3,
在Rt△AOH中,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴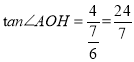 ,
,
∴∠AOH=74°,
∴∠AOH>60°,
∴AE>半徑,
∴劣弧![]() 長度>半徑;
長度>半徑;
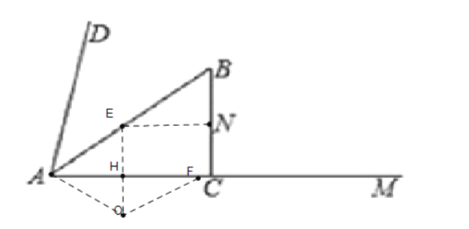
(3)當E運動到B點時,
t=10÷5=2,
∴AF=2×8=16,
此時△AEF的內心記為G,
當A、E、F三點重合時,內心為A,
∴![]() 的內心運動的路徑長為AG,
的內心運動的路徑長為AG,
作GP⊥AE于點P,GQ⊥EF于點Q,
S△AEF=![]() ,
,
設CG=a,
∴S△AEF=S△AGF+S△AEG+S△FEG,
∴![]() ,
,
解得:![]() ,
,
在Rt△ACG中,
![]() ,即
,即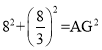 ,
,
∴AG=![]() ,
,
∴![]() 的內心運動的路徑長為
的內心運動的路徑長為![]() ;
;
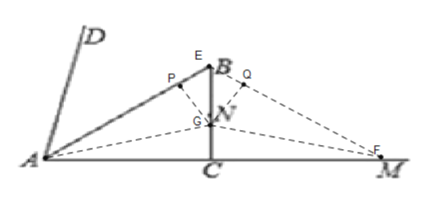
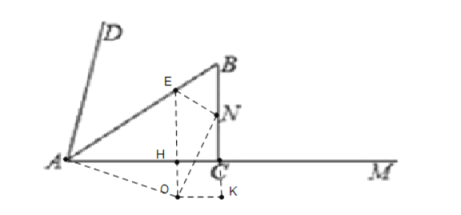
(4)分別討論兩種極限位置,
①當MN與![]() 相切時,
相切時,
由(2)知,t=1;
②當N在圓上時,即ON為半徑,如圖所示:
則OE=ON,
∴AH=4t,EH=3t,
設半徑為x,
則在Rt△AOH中,![]()
![]() ,
,
解得:![]() ,
,
∴CK=OH=![]() ,
,
在Rt△OKN中,
![]() ,
,
∴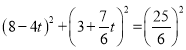 ,
,
解得:![]() ,
,
∴線段![]() 與
與![]() 有兩個公共點時,
有兩個公共點時,![]() 的取值范圍為
的取值范圍為![]() .
.


科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
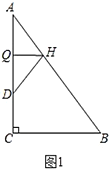
(1)如圖1,折疊![]() 使點
使點![]() 落在
落在![]() 邊上的點
邊上的點![]() 處,折痕交
處,折痕交![]() 、
、![]() 分別于點
分別于點![]() 、
、![]() ,若
,若![]() ,則
,則![]() ________.
________.
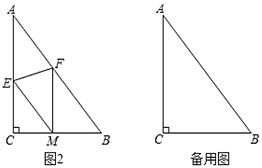
(2)如圖2,折疊![]() 使點
使點![]() 落在
落在![]() 邊上的點
邊上的點![]() 處,折痕交
處,折痕交![]() 、
、![]() 分別于點
分別于點![]() 、
、![]() .若
.若![]() ,求證:四邊形
,求證:四邊形![]() 是菱形;
是菱形;
(3)在(1)(2)的條件下,線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出
相似?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,點A的坐標為(0,8),點 B(b,t)在直線x=b上運動,點D、E、F分別為OB、0A、AB的中點,其中b是大于零的常數.
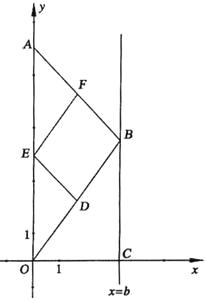
(1)判斷四邊形DEFB的形狀.并證明你的結論;
(2)試求四邊形DEFB的面積S與b的關系式;
(3)設直線x=b與x軸交于點C,問:四邊形DEFB能不能是矩形?若能.求出t的值;若不能,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
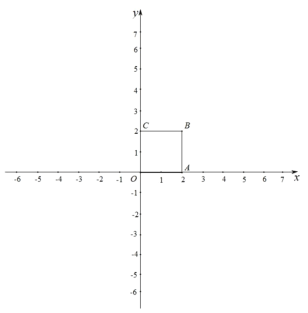
【題目】對于平面內的點 P 和圖形 M,給出如下定義:以點 P 為圓心,以 r 為半徑作⊙P,使得圖形 M 上的所有點都在⊙P 的內部(或邊上),當 r 最小時,稱⊙P 為圖形 M 的 P 點 控制圓,此時,⊙P 的半徑稱為圖形 M 的 P 點控制半徑.已知,在平面直角坐標系中, 正方形 OABC 的位置如圖所示,其中點 B(2,2)
(1)已知點 D(1,0),正方形 OABC 的 D 點控制半徑為 r1,正方形 OABC 的 A 點 控制半徑為 r2,請比較大小:r1 r2;
(2)連接 OB,點 F 是線段 OB 上的點,直線 l:y= ![]() x+b;若存在正方形 OABC 的 F點控制圓與直線 l 有兩個交點,求 b 的取值范圍.
x+b;若存在正方形 OABC 的 F點控制圓與直線 l 有兩個交點,求 b 的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解密數學魔術:魔術師請觀眾心想一個數,然后將這個數按以下步驟操作:
![]()
魔術師能立刻說出觀眾想的那個數.
(1)如果小玲想的數是![]() ,請你通過計算幫助她告訴魔術師的結果;
,請你通過計算幫助她告訴魔術師的結果;
(2)如果小明想了一個數計算后,告訴魔術師結果為85,那么魔術師立刻說出小明想的那個數是:__________;
(3)觀眾又進行了幾次嘗試,魔術師都能立刻說出他們想的那個數.若設觀眾心想的數為![]() ,請你按照魔術師要求的運算過程列代數式并化簡,再用一句話說出這個魔術的奧妙.
,請你按照魔術師要求的運算過程列代數式并化簡,再用一句話說出這個魔術的奧妙.
查看答案和解析>>
科目:初中數學 來源: 題型:
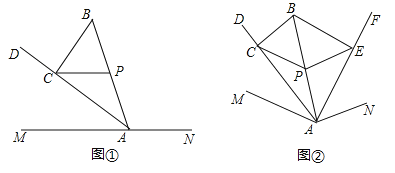
【題目】探究:如圖①,點![]() 在直線
在直線![]() 上,點
上,點![]() 在直線
在直線![]() 外,連結
外,連結![]() .過線段
.過線段![]() 的中點
的中點![]() 作
作![]() ,交
,交![]() 的平分線
的平分線![]() 于點
于點![]() ,連結
,連結![]() .求證:
.求證:![]() .
.
應用:如圖②,點![]() 在
在![]() 內部,連結
內部,連結![]() .過線段
.過線段![]() 的中點
的中點![]() 作
作![]() ,交
,交![]() 的平分線
的平分線![]() 于點
于點![]() ;作
;作![]() ,交
,交![]() 的平分線
的平分線![]() 于點
于點![]() ,連結
,連結![]() 、
、![]() .若
.若![]() ,則
,則![]() 的大小為多少度.
的大小為多少度.
查看答案和解析>>
科目:初中數學 來源: 題型:
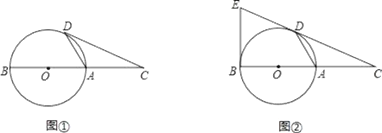
【題目】已知點C為直徑BA的延長線上一點,CD切⊙O于點D,
(Ⅰ)如圖①,若∠CDA=26°,求∠DAB的度數;
(Ⅱ)如圖②,過點B作⊙O的切線交CD的延長線于點E,若⊙O的半徑為3,BC=10,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形紙片ABCD中,已知AD=8,AB=6,E是邊BC上的點,以AE為折痕折疊紙片,使點B落在點F處,連接FC,當△EFC為直角三角形時,BE的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c經過A(﹣1,0)、B(5,0)、C(0,﹣5)三點.
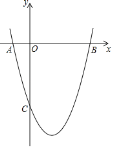
(1)求拋物線的解析式和頂點坐標;
(2)當0<x<5時,y的取值范圍為 ;
(3)點P為拋物線上一點,若S△PAB=21,直接寫出點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com