
【題目】已知△ABC為等邊三角形,P是直線AC上一點,AD⊥BP于D,以AD為邊作等邊△ADE(D,E在直線AC異側).
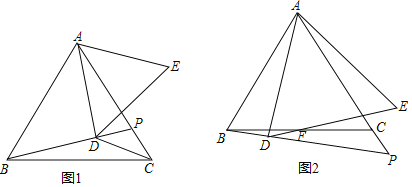
(1)如圖1,若點P在邊AC上,連CD,且∠BDC=150°,則![]() = ;(直接寫結果)
= ;(直接寫結果)
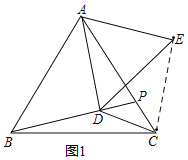
(2)如圖2,若點P在AC延長線上,DE交BC于F求證:BF=CF;
(3)在圖2中,若∠PBC=15°,AB=![]() ,請直接寫出CP的長 .
,請直接寫出CP的長 .
【答案】(1)![]() (2)證明見解析(3)
(2)證明見解析(3)![]()
【解析】
(1)由題意可證△ABD≌△ACE,可得BD=CE,∠ABD=∠ACE,即可求∠EDC=60°,∠EDC=90°,則可得![]() 的值;
的值;
(2)過點CM∥BD交DE于點M,連接CE,由題意可證△ABD≌△ACE,可得BD=CE,∠AEC=∠ADB=90°,可求∠DEC=∠EMC=30°,可得MC=EC=BD,
則可證△BDF≌△CMF,可得BF=CF;
(3)作∠ABG=∠BAD,交AD于點G,由題意可求∠ABG=∠BAG=15°,可得∠BGD=30°,BG=AG,則可得BG=2BD,GD=![]() BD,AD=
BD,AD=![]() BD+2BD,根據勾股定理可求BD=1,AD=2+
BD+2BD,根據勾股定理可求BD=1,AD=2+![]() ,即可求AP的長,則可求CP的長.
,即可求AP的長,則可求CP的長.
(1)如圖:連接CE
∵△ABC,△ADE是等邊三角形,
∴AB=AC,AD=AE,∠DAE=∠BAC=60°,
∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ADB=90°,∠BDC=150°,∠ADE=60°,
∴∠EDC=60°,
∵∠BDC=∠BPC+∠ACD=∠BAC+∠ABD+∠ACD=60°+∠ACE+∠ACD=60°+∠ECD=150°
∴∠ECD=90°,
∴tan∠EDC=![]() ,
,
∴![]() ;
;
(2)如圖:過點CM∥BD交DE于點M,連接CE
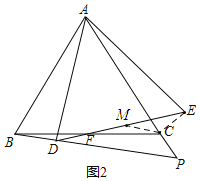
∵△ABC和△ADE是等邊三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°=∠ADE=∠AED,
∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△ABD≌△ACE(ASA),
∴BD=CE,∠AEC=∠ADB=90°,
∵∠BDE=∠ADB+∠ADE,∠DEC=∠AEC-∠AED,
∴∠BDE=150°,∠DEC=30°,
∵MC∥BD,
∴∠DMC=∠BDE=150°,
∴∠EMC=30°,
∴∠DEC=∠EMC,
∴MC=CE,
∴BD=CM,且∠BDE=∠CMD,∠BFD=∠CFM,
∴△BDF≌△CMF(AAS),
∴CF=BF,
(3)如圖:作∠ABG=∠BAD,交AD于點G
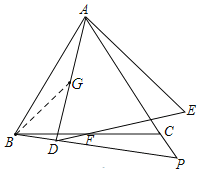
∵∠ABC=60°,∠PBC=15°,AD⊥BD,
∴∠DAB=15°,
∵∠ABG=∠BAD,
∴∠ABG=∠BAG=15°,
∴∠BGD=30°,BG=AG,
∴BG=2BD,GD=![]() BD,
BD,
∴AD=![]() BD+2BD,
BD+2BD,
在Rt△ABD中,AB2=BD2+AD2.
∴(![]() +
+![]() )2=(
)2=(![]() +2)2 BD2+BD2.
+2)2 BD2+BD2.
∴BD=1,
∴AD=2+![]() ,
,
∵∠BAD=15°,∠BAC=60°,
∴∠DAP=45°,且AD⊥BD,
∴AP=![]() AD=2
AD=2![]() +
+![]() ,
,
∵CP=AP-AC=AP-AB=2![]() +
+![]() -(
-(![]() +
+![]() ),
),
∴CP=![]() .
.
故答案為![]() .
.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:初中數學 來源: 題型:
【題目】小明在課外學習時遇到這樣一個問題:
定義:如果二次函數y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常數)與y=a2x2+b2x+c2
(a2≠0,a2,b2,c2是常數)滿足a1+a2=0,b1=b2,c1+c2=0,則稱這兩個函數互為“旋轉函數”.求y=-2x2+5x-3函數的“旋轉函數”.
小明是這樣思考的:由y=-2x2+5x-3函數可知,a1=-2,b1=5,c1=-3,根據a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2就能確定這個函數的“旋轉函數”.
請參考小明的方法解決下面的問題:
(1)寫出函數y=-2x2+5x-3的“旋轉函數”;
(2)若函數y1=x2+![]() x-n與y2=-x2-mx-2互為“旋轉函數”,求(m+n)2019的值;
x-n與y2=-x2-mx-2互為“旋轉函數”,求(m+n)2019的值;
(3)已知函數y=![]() (x-2)(x+3)的圖像與
(x-2)(x+3)的圖像與![]() 軸交于A、B兩點,與y軸交于點C,點A、B、C關于原點的對稱點分別是A1、B1、C1,試證明經過點A1、B1、C1的二次函數與函數y=
軸交于A、B兩點,與y軸交于點C,點A、B、C關于原點的對稱點分別是A1、B1、C1,試證明經過點A1、B1、C1的二次函數與函數y=![]() (x-2)(x+3)互為“旋轉函數”.
(x-2)(x+3)互為“旋轉函數”.
查看答案和解析>>
科目:初中數學 來源: 題型:
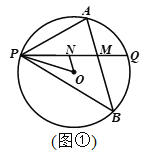
【題目】已知P是⊙O上一點,過點P作不過圓心的弦PQ,在劣弧PQ和優弧PQ上分別有動點A、B(不與P,Q重合),連接AP、BP. 若∠APQ=∠BPQ.
(1)如圖1,當∠APQ=45°,AP=1,BP=2![]() 時,求⊙O的半徑;
時,求⊙O的半徑;
(2)如圖2,選接AB,交PQ于點M,點N在線段PM上(不與P、M重合),連接ON、OP,若∠NOP+2∠OPN=90°,探究直線AB與ON的位置關系,并證明.
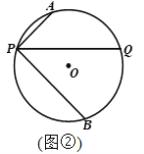
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在路燈下,小明的身高如圖中線段AB所示,他在地面上的影子如圖中線段AC所示,小亮的身高如圖中線段FG所示,路燈燈泡在線段DE上.

(1)請你確定燈泡所在的位置,并畫出小亮在燈光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子長AC=1.4m,且他到路燈的距離AD=2.1m,求燈泡的高.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是一座古拱橋的截面圖,拱橋橋洞的上沿是拋物線形狀,當水面的寬度為10m時,橋洞與水面
的最大距離是5m.
(1)經過討論,同學們得出三種建立平面直角坐標系的方案(如下圖)
你選擇的方案是_____(填方案一,方案二,或方案三),則B點坐標是______,求出你所選方案中的拋物線的表達式;
(2)因為上游水庫泄洪,水面寬度變為6m,求水面上漲的高度.


查看答案和解析>>
科目:初中數學 來源: 題型:
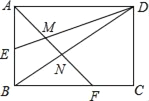
【題目】如圖,矩形ABCD的邊長AD=6,AB=4,E為AB的中點,F在邊BC上,且BF=2FC,AF分別與DE、DB相交于點M,N,則MN的長為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
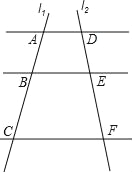
【題目】如圖,已知AD∥BE∥CF,它們依次交直線l1、l2于點A、B、C和點D、E、F,![]() ,AC=14;
,AC=14;
(1)求AB、BC的長;
(2)如果AD=7,CF=14,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
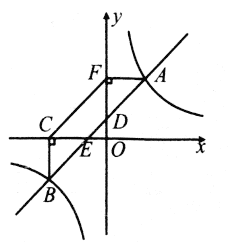
【題目】如圖,一次函數![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() ,且與反比例函數
,且與反比例函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點.
兩點.
(1)分別求出一次函數與反比例函數的表達式;
(2)過點![]() 作
作![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,求四邊形
,求四邊形![]() 的面積
的面積![]() ;
;
(3)當![]() 時,
時,![]() 的取值范圍是________.
的取值范圍是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
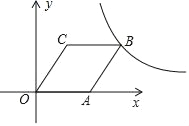
【題目】如圖,在平面直角坐標系中,點O為坐標原點,菱形OABC的頂點A在x軸的正半軸上,頂點C的坐標為(1,![]() ).
).
(1)求圖象過點B的反比例函數的解析式;
(2)求圖象過點A,B的一次函數的解析式;
(3)在第一象限內,當以上所求一次函數的圖象在所求反比例函數的圖象下方時,請直接寫出自變量x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com